• 정렬되지 않은 리스트에서 주어진 키가 존재하는가? - 순차 탐색
  • 정렬된 리스트에서 주어진 키가 존재하는가? - 이분 검색
  • 이분검색의 알고리즘 설계방식: 분할정복(Divide-and-Conquer)
      :point_right: 정렬된 리스트 S에 어떤 키 x가 존재하는가?
  :point_right: 존재하면 S에서 x의 위치, 아니면 -1을 리턴

    S의 정가운데 원소와 x를 비교하여 같으면 해당 위치를 리턴 아니라면,
    Divide: 정 가운데 원소를 기준으로 S를 두개의 리스트로 분할
    Conquer: x가 정가운데 원소보다 크면 오른쪽, 작으면 왼쪽을 재귀 호출
    Obtain: 선택한 리스트에서 얻은 답을 리턴

파이썬으로 이분검색

1
2
3
4
5
6
7
8
9
10
11
def location (S, low, high):
    if (low > high):
        return 0
    else:
        mid = (low + high) // 2
        if (x == S[mid]):
            return mid
        elif (x < S[mid]):
            return location(S, low, mid -1)
        else:
            return location(S, mid+1, high)

자바스크립트로 이분검색

1
2
3
4
5
6
7
8
9
10
function location(arr, low = 0, high = arr.length) {     
    if(low > high) 
        return 0
    else {
        let mid = Math.floor((low + high) / 2);
        if(x === arr[mid]) return mid;
        else if (x < arr[mid]) return location(arr, low, mid-1);
        else return location(arr, mid+1, high);
    }
}

강의 내에서 x값은 전역변수를 사용하였음

합병정렬

  • 합병정렬의 알고리즘 설계방식: 분할정복(Divide-and-Conquer)

    Divide: 원소가 n개인 S를 n/2개의 원소를 가진 두 개의 리스트로 분할
    Conquer: 왼쪽의 리스트와 오른쪽의 리스트를 각각 재귀적으로 합병정렬
    Obtain: 각각 정렬된 두 개의 리스트를 정렬된 하나의 리스트로 합병하여 리턴


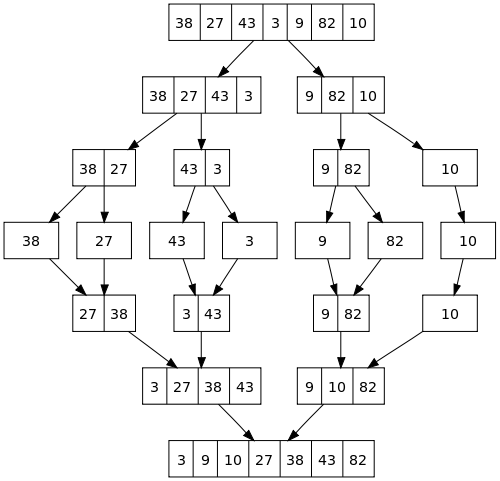
합병정렬 예시

파이썬으로 합병정렬

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def mergesort (S):
    n = len(S)
    if (n <= 1):
        return S
    else:
        mid = n // 2
        U = mergesort(S[0 : mid])
        V = mergesort(S[mid: n])
        return merge(U, V)

def merge(U, V):
    S = []
    i = j = 0
    while (i < len(U) and j < len(V)):
        if(U[i] < V[j]):
            S.append(U[i])
            i += 1
        else:
            S.append(V[j])
            j += 1
    if (i < len(U)):
        S += U[i : len(U)]
    else:
        S += V[j : len(V)]
    return S

자바스크립트로 합병정렬

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
function mergesort (arr) {
    if(arr.length === 1) return arr;
    
    let mid = Math.floor(arr.length/2);
    let leftSide = arr.slice(0, mid)
    let rightSide = arr.slice(mid)
    
    return merge(mergesort(leftSide), mergesort(rightSide));
    
}

function merge(left, right) {
    let result = [];
    while (left.length !== 0 && right.length !== 0) {
		left[0] <= right[0] 
        ? result.push(left.shift()) 
        : result.push(right.shift());
	}

    return [...result, ...left, ...right];
}
  • 합병정렬의 문제점
    • 배열을 추가적으로 사용하게 됨 → 메모리 사용의 비효율성

합병정렬의 효율화

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def mergesort2 (S, low, high):
    if(low < high):
        mid = (low + high) // 2
        mergesort2(S, low, mid)
        mergesort2(S, mid + 1, high)
        merge2(S, low, mid, high)

def merge2(S, low, mid, high):
    U = []
    i = low
    j = mid +1
    while (i <= mid and j <= high):
        if (S[i] < S[j]):
            U.append(S[i])
            i += 1
        else:
            U.append(S[j])
            j += 1
    if (i <= mid):
        U += S[i : mid + 1]
    else:
        U += S[j : high + 1]
    for k in range(low, high +1):
        S[k] = U[k -low]

자바스크립트로 합병정렬 조금 더 생각해보기

1
2
3
4
5
6
7
8
9
10
11
12
// 파이썬처럼 배열을 덜 정의하면서 효율적으로 구현하는 법은 더 검색해볼 것
function mergesort (arr) {
    if(arr.length === 1) return arr;
    
    let mid = Math.floor(arr.length/2);
    let leftSide = arr.splice(0, mid)
    // splice함수를 사용하면 arr를 조작하므로 
    // arr에는 자동적으로 rightSide만 남게 됨

    return merge(mergesort(leftSide), mergesort(arr));    
}
// merge 함수는 상동하므로 생략