21-02-22 알고리즘 기초강의(2)

최단경로와 플로이드 알고리즘

최단 경로 문제
- 주어진 그래프에서 모든 정점의 쌍에 대한 최단 경로를 구하기
- G = (V, E)일 때, G는 Graph, V는 Vertex set, E는 Edge set
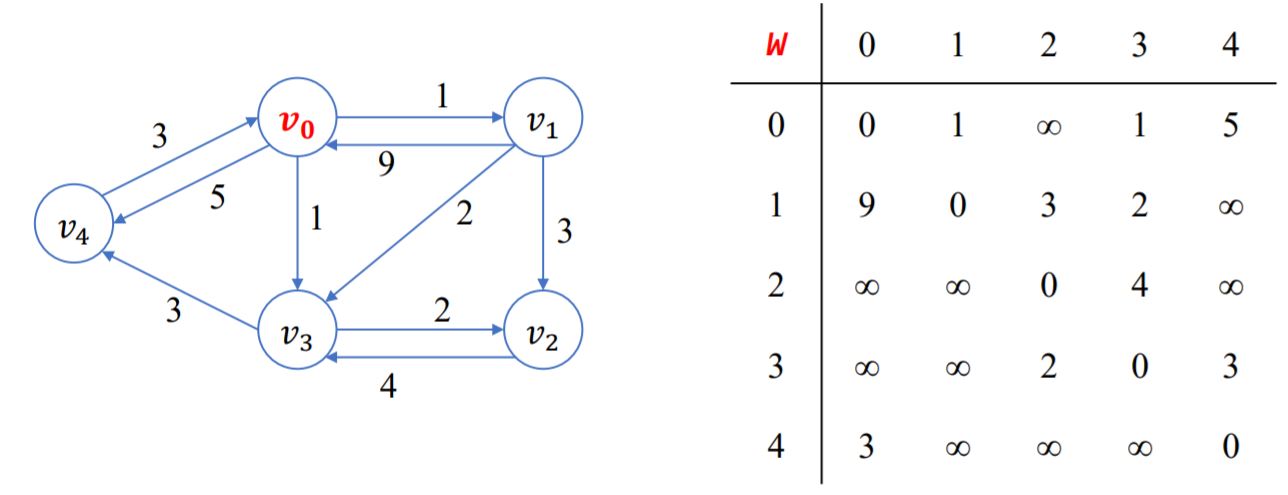
- G는 방향성, 가중치 그래프로, V1 -6→ V3 와 같은 것을 표로 표현
- 최단 경로는 단순 경로: 같은 정점을 두 번 거치지 않음
  
  figure 01) 그래프로 표현되는 경우
최단 경로 문제의 이해
- Brute-force로 해결하기
  - 각 정점들에서 다른 정점으로 가는 모든 경로를 구하고
  - 그 경로들 중에서 가장 짧은 경로를 찾는 방법
  - 효율성 분석: 모든 정점간 간선이 존재하면 O(n!)만큼 복잡해진다
- 최단 경로 문제는 최적화 문제(optimization problem)
  - 최적화 문제는 하나 이상의 해답 후보가 있을 수 있음
  - 그 중에 가장 최적의 값을 가진 해답을 찾는 문제
- Dynamic programming으로 해결하기
  1. 재귀 관계식을 찾는다
  - D: 각 정점의 쌍이 가지는 최단 경로의 길이를 나타내는 행렬
  - D[i][j]: Vi에서 Vj로 가는 최단 경로의 길이
  - 인접 행렬 W에서 최단 경로의 행렬 D와의 재귀 관계식을 구해야 함
  1. 상향식 방법으로 해답을 구한다
  - D^0^ = W로 초기화, 최종 목표는 D^n^ = D (D^0^, D^1^,…, D^n^)
  1. 행렬의 이해
  - D^k^ : k개의 중간 정점을 지나는 최단 경로 길이의 행렬
  - D^k^[i][j] : vi에서 vj로 k개의 중간 정점을 지나는 최단 경로 길이
  - D^0^ : 다른 어떤 정점도 지나지 않는 최단 경로의 길이 (=W)
  - D^n^ : 다른 모든 정점을 지날 수 있는 최단 경로의 길이 (=D)
  1. 재귀 관계식 구하기
  - D^0^ = W, D^k^는 D^k-1^로부터 구함 (1 ≤ k ≤ n)
  - D^k-1^[i][j]: vi에서 vj로 k-1개의 중간 정점을 지남
  - D^k^[i][j]의 경우
    → 하나의 정점을 더 지나도 최단경로가 없는 경우
    D^k^[i][j] = D^k-1^[i][j]
    → 하나의 정점을 더 지나면 최단경로가 되는 경우
    D^k^[i][j] = D^k-1^[i][k] + D^k-1^[k][j]
    (임의의 경로 = v가 갖는 열 내 k 번째 가중치 + 해당 k번째 v가 갖는 가중치)
  1. 최단 경로의 재귀 관계식
    D^k^[i][j] = min(D^k-1^[i][j], D^k-1^[i][k] + D^k-1^[k][j])

파이썬으로 플로이드 알고리즘

def floyd (W):
    D = W
    n = len(W)
    for k in range(n):
        for i in range(n):
            for j in range(n):
                D[i][j] = min(D[i][j], D[i][k] + D[k][j])
    return D

자바스크립트로 플로이드 알고리즘

const floyd = W => {
    let arr = [...W];
    let n = W.length;
    for (let k = 0; k < n; k++) 
        for (let i = 0; i < n; i++)  
            for (let j = 0; j < n; j++) 
                arr[i][j] = Math.min(arr[i][j], arr[i][k] + arr[k][j])
    return arr
}

최단 길이는 구했으나, 최단 경로는?
- 최단 경로를 구하기 위해서는 과정을 기록해야 함
- P[i][j]: vi에서 vj로 가는 최단 경로가 거쳐야 하는 새로운 정점
  - vi에서 vj로 가는 최단 경로 중간에 놓여있는 정점이 최소한 하나 있다면 그 놓여있는 정점 중에서 가장 큰 인덱스
  - 최단 경로의 중간에 놓여있는 정점이 없는 경우에는 -1
- P[i][j] 값이 -1이라면 간선이 최단경로
- P[i][j] = k 라면 탐색해서 가장 길이가 짧은 값의 index를 탐색해야 함

파이썬으로 최단 경로 구하기

def floyd (W):
    n = len(W)
    D = W
    P = [[-1] * n for _ in range(n)]
    for k in range(n):
        for i in range(n):
            for j in range(n):
                if (D[i][j] > D[i][k] + D[k][j]):
                    D[i][j] = D[i][k] + D[k][j]
                    P[i][j] = k
    return D, P

def path (P, u, v):
    if(P[u][v] != -1):
        path(P, u, P[u][v])
        print('v%d' %(P[u][v]), end = '-> ')
        path(P, P[u][v], v)

D, P = floyd2(W)
for i in range(len(D)):
    print(D[i])
for i in range(len(P)):
    print(P[i])

자바스크립트로 최단 경로 구하기

const floydWarshall2 = nodes => {
    let n = nodes.length;
    let arr = [...nodes];
    let route = Array.from(Array(n), () => Array(n).fill(-1));
    for (let k = 0; k < n; k++) 
        for (let i = 0; i < n; i++)  
            for (let j = 0; j < n; j++) {
                if (arr[i][j] > arr[i][k] + arr[k][j]) {
                 arr[i][j] = arr[i][k] + arr[k][j];
                 route[i][j] = k;
                } 
            }
    return { arr: arr, route: route };
}


let { arr, route } = floydWarshall2(nodes)

let str = `v${u}` // u값을 미리 정의한다면 이렇게 사용할 수 있다
const path = (route, u, v) => {
    if (route[u][v] !== -1) {
        path(route, u, route[u][v])
        str += ` → v${route[u][v]}`
        path(route, route[u][v], v);        
    } 
    return str + ` → v${v}`
}

from(itarable obj, map function) 함수를 사용해야 함 fill 함수를 사용하게 될 경우 배열 내 채워지는 모든 배열들의 주소값이 동일한 주소로 입력되기 때문

21-02-22 알고리즘 기초강의(2)

최단경로와 플로이드 알고리즘

Harry Kim