진법을 변환하기

  • A진법 수 N을 입력 받아 B진법 수로 변환하는 문제
  • Horner’s Method

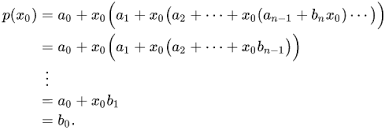
    → 해시 문제나 긴자리수 진법 변환 문제에 사용됨
  • 2진수를 10진수로 변환하기
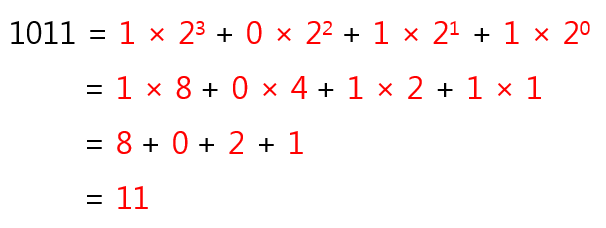
  • 예1) 2진법 11010을 8진법으로 바꾸어보자
    → char str[] = “11010”
    (의미는 없지만 JS에서는 let str = Number(10110).toString()로 표현가능함)

d = d * 2 + ‘1’ - ‘0’; // d(3) = 1 * 2 + 1
d = 02 + 1 = 1
d = 12 + 1 = 3
d = 32 + 0 = 13
d = 62 + 1 = 13
d = 13*2 + 1 = 26

  • 10진법을 먼저 구하고 10진법 26을 8진법으로 바꾸기

    38 + 2 ``26/88 + 26%8(0*8 +**3**) * 8 + **2**(3/88 + 3%8)*8 + 26%8``
    *    32** (Octet)

  • 예2) 10진법 2543을 16진법으로 바꾸기

    158 * 16 + ‘F’ 2543/16 * 16 + 2543%16 // 158*16 + 15
    (916 + ‘E’) * 16 + ‘F’ ``(158/16)*16 + 158%16 + ‘F’ // 916 + 14 + ‘F’``
    ((016 + 9) * 16 + *‘E’*) * 16 + *‘F’** = 9EF (Hexadecimal)

자바스크립트의 진법 변환은 매우 간단하기 때문에 별도의 코드는 첨부하지 않음

1
2
3
4
let value = 10;
value.toString(2) // 2진법으로 변경
let binary = 1010;
Number.parseInt(binary, 2) // 10진법으로 변경

앞뒤 같은 제곱

  • N(1≤N≤300)중에서 N의 제곱값을 B(2≤B≤20)진수로 바꿨을 때 앞뒤가 같은 수가 되는 N값과 N의 제곱값을 B진수로 바꾸는 문제 (단, 10보다 큰 숫자는 A~J로 표현)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
const changeNumBase = powNum => {
    let arr = [];
    for (let i = 1; i <= 300; i++) {
        arr.push(Math.pow(i, powNum))
    }
    arr = arr.filter(num => {
        return num.toString() === num.toString().split('').reverse().join('');
    })

   return arr;
}

const solution = () => {
    let arr = [];
    for (let i = 2; i <= 20; i++) {
        arr.push(changeNumBase(i));
    }
    return arr.filter(el => el.length > 1)
}

/* 출력 예시
[
  [     1,     4,     9,
      121,   484,   676,
    10201, 12321, 14641,
    40804, 44944, 69696
  ],
  [ 1, 8, 343, 1331, 1030301, 1367631 ],
  [ 1, 14641, 104060401 ]
]
*/