21-03-27 자바스크립트로 하는 자료구조와 알고리즘(2-01)

Mar 27, 2021 in 알고리즘, 서적

5장 연습문제 다시 보기

const findSumBetter = (arr, weight) => {
  let hashtable = {};
  for (let i = 0, arrLength = arr.length; i < arrLength; i++) {
    let currentElement = arr[i];
    let difference = weight - currentElement;

    if (hashtable[currentElement] != undefined) {
      return [i, hashTable[currentElement]];
    } else {
      hashtable[difference] = i;
    }
  }
  return -1;
};

Comment and share

21-03-24 알고리즘 문제풀기 및 노트 정리

Mar 24, 2021 in 알고리즘

스킬트리

해당 문제 링크

처음엔 각 스킬을 키로, 인덱스를 값으로 갖는 객체를 만들어 풀려 했으나 스킬트리 내 스킬들 인덱스 비교가 어려워서 다른 방법을 찾다가 정규식으로 처리하는 방법을 찾음

function solution(skill, skill_trees) {
    let regex = new RegExp(`[^${skill}]`, 'g'); // 정규식으로 skill에 해당하지 않는(^) 글자를 찾게끔하기
    let isPossible = skill_trees.map(eachTree => eachTree.replace(regex, '')) // replace를 통해 스킬이 아닌것들을 죄다 빈 문자열로 변환
                                .filter(each => skill.substring(0, each.length) === each) 
                                // 정규식으로 필터링된 각 스킬트리를 substring으로 원래 스킬을 필터링된 문자열의 길이만큼 잘라내고 그 값이 스킬트리와 같은지 비교
    return isPossible.length; // isPossible 배열 내에는 배울 수 있는 스킬만 남을 것이므로 배열의 길이를 리턴
}

괄호 변환

해당 문제 링크

1. 입력이 빈 문자열인 경우, 빈 문자열을 반환합니다. 
2. 문자열 w를 두 "균형잡힌 괄호 문자열" u, v로 분리합니다. 단, u는 "균형잡힌 괄호 문자열"로 더 이상 분리할 수 없어야 하며, v는 빈 문자열이 될 수 있습니다. 
3. 문자열 u가 "올바른 괄호 문자열" 이라면 문자열 v에 대해 1단계부터 다시 수행합니다. 
  3-1. 수행한 결과 문자열을 u에 이어 붙인 후 반환합니다. 
4. 문자열 u가 "올바른 괄호 문자열"이 아니라면 아래 과정을 수행합니다. 
  4-1. 빈 문자열에 첫 번째 문자로 '('를 붙입니다. 
  4-2. 문자열 v에 대해 1단계부터 재귀적으로 수행한 결과 문자열을 이어 붙입니다. 
  4-3. ')'를 다시 붙입니다. 
  4-4. u의 첫 번째와 마지막 문자를 제거하고, 나머지 문자열의 괄호 방향을 뒤집어서 뒤에 붙입니다. 
  4-5. 생성된 문자열을 반환합니다.

function solution(p) {
    if (p === '') return p; // 1. 입력이 빈 문자열인 경우, 빈 문자열을 반환합니다. 

    let left = 0, right = 0, pIndex = 0; // 레벨 1의 올바른 괄호처럼 left와 right를 나누기
    let isBalanced = true; // "균형잡힌 괄호 문자열"의 flag 변수

    do {
        if (p[pIndex] === '(') left++; 
        else right++;
        
        if(right > left) 
            isBalanced = false;
        pIndex++;
    } while (left !== right)
    
    let u = p.substr(0, pIndex);
    let v = p.substr(pIndex);

    if(isBalanced) {
        return u + solution(v);
    } else {
        u = u.substr(1, u.length - 2).replace(/[\(]|[\)]/g, a => a === ')' ? '(' : ')');
        v = `(${solution(v)})`;
            return v +u;
    }
}

재귀적으로 구현하는 법에 대해서 완벽하게 이해하지 못해서 다른 사람 풀이를 참고함

function solution(p) {
  if (p.length < 1) return ""; // 1번

  let balance = 0; // 재귀적으로 호출될 때마다 0으로 초기화됨
  let pivot = 0; 
  do { 
      balance += p[pivot++] === "(" ? 1 : -1  // 좌측 괄호라면 1을 아니라면 -1을 더함  
  } while (balance !== 0); // 0이라면 "균형잡힌 괄호 문자열"

  const u = p.slice(0, pivot); // balance가 0이 아니라면 문자열 w를 두 "균형잡힌 괄호 문자열" u, v로 분리
  const v = solution(p.slice(pivot, p.length)); // v는 1부터 다시 수행해야 하므로 재귀적으로 함수를 호출 (u로 나눠진 부분 다음부터)

  if (u[0] === "(" && u[u.length - 1] == ")")  // 첫 괄호와 마지막 괄호를 검사해 "올바른 괄호 문자열"인지 확인
    return u + v; 
  else 
    return "(" + v + ")" + reverse(u); 
}

function reverse(str) {
  return str.slice(1, str.length - 1) // u의 첫 번째와 마지막 문자를 제거
            .split("")
            .map((c) => (c === "(" ? ")" : "(")) // 나머지 문자열의 괄호 방향을 뒤집어서 뒤에 붙임
            .join(""); // 다시 문자열로 join하여 리턴
}

소수 찾기(레벨2)

해당 문제 링크

function solution(numbers) {
   let answer = 0;
   let primeNums = [];

   let splitedNumbers = numbers.split('')

   const isPrime = num => {
       let count = 0;
       for(let i = 1; i <= num; i++) {
           if (num % i === 0) {
               count++;
           }
           if (count >= 3) {
               break;
           }
       }
       if (count === 2 && !primeNums.includes(num)) {
           primeNums.push(num);
       }
   }

   const createNumbers = (arr, str) => {
       if (arr.length > 0) {
           for (let i = 0; i < arr.length; i++) {
               const temp = [...arr];
               temp.splice(i, 1);
               createNumbers(temp, str + arr[i])
           }
       }

       if (str.length > 0) {
           isPrime(+str);
       }
   }

   createNumbers(splitedNumbers, '');

   answer = primeNums.length;
   return answer;
}

Comment and share

21-03-23 알고리즘 문제풀기 및 노트 정리

Mar 23, 2021 in 알고리즘

소수 만들기

해당 문제 링크

에라토스테네스의 체를 세 정수의 최대값인 2997까지 구함
nums 배열을 돌며 세 정수의 합을 구해 배열에 push
해당 배열 값을 인덱스로 가지는 에라토스테네스의 체의 값이 false가 아니라면 answer값을 증가시킨다

function solution(nums) {
   let combination = [];
    let answer = 0;
    let primeNums = [];

    for(let i = 2; i <= 2997; i++){ 
        if(primeNums[i] == false) 
            continue; 
        for(let k = i + i; k <= 2997; k += i) { 
            primeNums[k] = false; 
        } 
    }


    for (let i = 0; i < nums.length; i++) {
        for (let j = i+1; j < nums.length; j++) {
            for (let k = j+1; k < nums.length; k++){
                let temp = nums[i]+nums[j]+nums[k];
                combination.push(temp);
            }
        }
    }

    for (let i = 0; i < combination.length; i++) {
        if(primeNums[combination[i]] !== false)
            answer++
    }
    return answer;
}

신규 아이디 추천

해당 문제 링크

1. 모든 대문자를 대응되는 소문자로 치환합니다.
2. 알파벳 소문자, 숫자, 빼기(-), 밑줄(_), 마침표(.)를 제외한 모든 문자를 제거합니다.
3. 마침표(.)가 2번 이상 연속된 부분을 하나의 마침표(.)로 치환합니다.
4. 마침표(.)가 처음이나 끝에 위치한다면 제거합니다.
5. 빈 문자열이라면, "a"를 대입합니다.
6. 길이가 16자 이상이면, 첫 15개의 문자를 제외한 나머지 문자들을 모두 제거합니다.
7. 만약 제거 후 마침표(.)가 끝에 위치한다면 끝에 위치한 마침표(.) 문자를 제거합니다.
8. 길이가 2자 이하라면, 마지막 문자를 길이가 3이 될 때까지 반복해서 끝에 붙입니다.

정규식을 사용해 1번부터 8번을 구현하기
4번, 5번을 모르겠어서 다른 분의 풀이를 참고함
정규식은 언제 봐도 어렵다…

function solution(new_id) {
    const answer = new_id
        .toLowerCase() // 1. 모두 소문자로 치환
        .replace(/[^\w-_.]/g, '') // 2. \w는 밑줄 문자를 포함한 영숫자 문자에 대응
        .replace(/\.{2,}/g, '.') // 3. \.{2,}로 2개 이상 연속된다면 '.'로 replace
        .replace(/^\.|\.$/g, '') // 4. 마침표가 처음과 끝에 있는지 확인 ^\.| \.$(^: 입력의 시작부분, $: 입력의 끝부분)
        .replace(/^$/, 'a') // 5. 시작(^)과 끝($)이 빈 문자열이라면 a로 replace
        .slice(0, 15).replace(/\.$/, ''); // 6, 7. slice로 15개 문자만 남기고 4번과 마찬가지로 \.$를 사용해 끝문자열의 마침표 삭제
    const len = answer.length;
    return len > 2 ? answer : answer + answer.charAt(len - 1).repeat(3 - len); // 8. 길이가 2보다 작다면 아이디 끝에 반복해서 붙이기
}

키패드 누르기

해당 문제 링크

맨 처음 왼손 엄지손가락은 * 키패드에 오른손 엄지손가락은 # 키패드 위치에서 시작하며, 엄지손가락을 사용하는 규칙은 다음과 같습니다.
1. 엄지손가락은 상하좌우 4가지 방향으로만 이동할 수 있으며 키패드 이동 한 칸은 거리로 1에 해당합니다.
2. 왼쪽 열의 3개의 숫자 1, 4, 7을 입력할 때는 왼손 엄지손가락을 사용합니다.
3. 오른쪽 열의 3개의 숫자 3, 6, 9를 입력할 때는 오른손 엄지손가락을 사용합니다.
4. 가운데 열의 4개의 숫자 2, 5, 8, 0을 입력할 때는 두 엄지손가락의 현재 키패드의 위치에서 더 가까운 엄지손가락을 사용합니다.
  4-1. 만약 두 엄지손가락의 거리가 같다면, 오른손잡이는 오른손 엄지손가락, 왼손잡이는 왼손 엄지손가락을 사용합니다.

간단한 해시 테이블을 사용하여 키의 위치를 할당하고 번호마다 왼손, 오른손의 현재 위치와의 거리를 구하여 이동하게 함

function solution (numbers, hand) {
    let answer = '';
    let keypad = { 
        1: [1,1], 2: [1,2], 3: [1,3], 
        4: [2,1], 5: [2,2], 6: [2,3], 
        7: [3,1], 8: [3,2], 9: [3,3], 
        '*': [4,1], 0: [4,2], '#': [4,3], 
    }
    let curLeft = keypad['*']
    let curRight = keypad['#']
    numbers.forEach(num => {
        let numPosition = keypad[num];

        if (numPosition[1] === 1) {
            curLeft = numPosition
            answer += 'L'
        } else if (numPosition[1] === 3) {
            curRight = numPosition
            answer += 'R'
        } else {
            let distanceLeft = calDistance(curLeft, numPosition)
            let distanceRight = calDistance(curRight, numPosition)

            if(distanceLeft === distanceRight) {
                if(hand === 'left') {
                    curLeft = numPosition;
                    answer += 'L'
                } else {
                    curRight = numPosition;
                    answer += 'R'
                }
            } else if (distanceLeft < distanceRight) {
                curLeft = numPosition;
                answer += 'L';
            } else {
                curRight = numPosition;
                answer += 'R';
            }
        }
    })

    return answer;
}

function calDistance(LeftOrRight, numPosition) {
    return Math.abs(LeftOrRight[0] - numPosition[0]) + Math.abs(LeftOrRight[1] - numPosition[1])
}

하샤드 수

해당 문제 링크

1분컷함…

function solution(x) {
    let sum = (''+x).split('').map(el => el*1).reduce((acc, cur) => acc+cur, 0);
    return x%sum === 0; 
}

Comment and share

21-03-22 알고리즘 문제풀기 및 노트 정리

Mar 22, 2021 in 알고리즘

크레인 인형뽑기 게임

해당 문제 링크

stack 배열을 생성하고 인형을 차례대로 담으면서 이전에 추가한 인형(stack의 마지막값)과 같은지 비교해서 score 계산을 해 주면 된다

function solution(board, moves) {
    let stack = [];
    let score = 0;
    for(let i = 0; i < moves.length; i++) {
        let move = moves[i]-1; // x좌표를 구함 (index는 1부터 시작하므로 1을 빼줌)
        for (let j = 0; j <board.length; j++){ // board 길이만큼 돌고
            if (board[j][move] !== 0) { // 해당 좌표에 있는 인형이 0이 아니고
                if (board[j][move] === stack[stack.length-1] && stack.length > 0){
                    // 이전에 추가한 인형과 값이 같다면 stack에서 빼주고 scoring하기
                    stack.pop();
                    score += 2
                } else {
                    // 값이 다르다면 그냥 stack에 push만 하기
                    stack.push(board[j][move])
                }
                // 해당 인형은 옮겼으니 0으로 바꿔 다시 선택하지 않도록 하기
                board[j][move] = 0;
                break;
            } 
        }
    }
    return score;
}

다트 게임

해당 문제 링크

처음에 혼자 풀 때 짰던 코드
스타상이 이전 점수에도 영향을 준다는 것을 고려하지 못함

또, 10점을 고려하기 위해 같은 코드가 반복되어 지저분해보임

function solution(dartResult) {
    let answer = 0;
    let split = dartResult.split('');
    let dartScore = 0, alphabet = '', powValue = 0, starOrSharp = '';
    while (split.length > 0){
        if (split[1] === '0') {
            dartScore = split.shift() * 10;
            split.shift();
            alphabet = split.shift();
            powValue = alphabet === 'S' ? 1 : alphabet === 'D' ? 2 : 3
            if (split[0] === '*' || split[0] === '#') {
                starOrSharp = split.shift() === '*' ? 2 : -1;
            } else {
                starOrSharp = 1;
            }
            answer += Math.pow(dartScore, powValue) * starOrSharp;
        } else if (split[1] !== '0') {
            dartScore = split.shift() * 1;
            alphabet = split.shift();
            powValue = alphabet === 'S' ? 1 : alphabet === 'D' ? 2 : 3
            if (split[0] === '*' || split[0] === '#') {
                starOrSharp = split.shift() === '*' ? 2 : -1;
            } else {
                starOrSharp = 1;
            }
            answer += Math.pow(dartScore, powValue) * starOrSharp;
        }
    }
    return answer;        
}

다른분 풀이
Object로 S, D, T값을 설정해 찾아 쓰는 방식은 O(1)로 가능하므로 보고 배워야겠다는 생각을 함

스택 구조를 만들고 스택 내에 점수를 하나씩 저장해놓고 스타상이 두번째에 온다면 스택 내 값을 수정하는 방식을 미처 생각치 못함


function solution(dartResult) {
    let stack = [];
    let score = {
        S: 1,
        D: 2,
        T: 3
    }
    let count = 0;
    const len = dartResult.length;
    
    for (let i = 0; i < len; i++) {
        let isChar = dartResult.charAt(i);
        if (+isChar != isChar) {
            if(score[isChar]) {
                stack.push(Math.pow(dartResult.slice(i - count, i), score[isChar]));
                count = 0;
            } else {
                const sharpOrStar = isChar === '*' ? 2 : -1;
                const stackLen = stack.length;
                if (sharpOrStar == 2 && stackLen > 1) {
                    stack[stackLen-2] = stack[stackLen-2] * sharpOrStar;
                }
                stack[stackLen-1] = stack[stackLen-1] * sharpOrStar;
            }
        } else {
            count++;
        }
    }
    return stack.reduce((acc, cur) => acc+ cur, 0)
}

폰켓몬

해당 문제 링크

처음에 든 생각은 그냥 set에 넣고 unique한 값만 뽑으면 되는 것 아닌가? 했음
문제에서 폰켓몬은 N/2마리를 선택해야 하므로 만약에 들어오는 배열의 길이를 반으로 나눈 값이 set의 사이즈보다 작다면 단순히 배열 길이를 반으로 나눈 값을 리턴하면 될 일이었음

function solution(nums) {
    let answer = 0;
    let set = new Set ();
    for(let number of nums){
        set.add(number);
    }

    if(set.size < nums.length/2) {
        answer = set.size;
    } else { 
        answer = nums.length/2;
    }
    return answer;
}

Comment and share

21-03-21 알고리즘 문제풀기 및 노트 정리

Mar 21, 2021 in 알고리즘

가장 큰 정사각형 찾기

해당 문제 링크

1과 0으로 채워진 표가 있고 1로 이루어진 정사각형 중 가장 큰 정사각형의 넓이를 리턴하는 문제

DP를 사용해 풀어야 한다

function solution (board) {
    let lengthY = board.length;
    let lengthX = board[0].length;
    let max = 0;
    if(lengthX < 2 || lengthY <2) {
        return 1;
    }

    for(let i = 1; i < lengthY; i++) {
        for(var j=1; j< lengthX; j++) {
            if(board[i][j] > 0) {
                board[i][j] = Math.min(
                    board[i-1][j-1], // 좌상단
                    board[i][j-1],   // 왼쪽
                    board[i-1][j])   // 오른쪽
                    + 1              // 현재값
            } 

            if(max < board[i][j]){
                max = board[i][j]
            }
        }
    }
    return Math.pow(max, 2)
}

다음 큰 숫자

해당 문제 링크

1
2
3

조건 1. n의 다음 큰 숫자는 n보다 큰 자연수 입니다.
조건 2. n의 다음 큰 숫자와 n은 2진수로 변환했을 때 1의 갯수가 같습니다.
조건 3. n의 다음 큰 숫자는 조건 1, 2를 만족하는 수 중 가장 작은 수 입니다.

내 풀이

function solution (n) {
    let largeNumber = n; // 나중에 리턴할 값
    let binary = n.toString(2).split(''); // n을 2진수로 바꾸고
    let cntOne = binary.filter(num => parseInt(num,10) > 0).length; // 1의 갯수를 filter하여 카운트
    
    while(true) {
        largeNumber++; // 값을 증가시키고
        let lnBinary = largeNumber.toString(2).split('') // 같은 방법으로 2진수로 변환하고
        let cntThisOne = lnBinary.filter(num => parseInt(num, 10) > 0).length; // 1의 갯수를 같은 방법으로 카운트
        if (cntThisOne === cntOne) // 만약에 n의 이진수가 갖는 1의 개수가 원래 값의 1의 개수랑 같다면 빠져나가기
            break;
    }
    return largeNumber;
}

시프트 연산자를 사용한 해법

function nextBigNumber(n) {
    var i, j;
    for (i = 0; !(n & 1); i++) {
        n = n >> 1; 
        } // 1을 찾을때까지 우로 쉬프트, 쉬프트 횟수 = i
    for (j = 0; n & 1; i++, j++) {
        n = n >> 1; 
        } // 0을 찾을때까지 우로 쉬프트, 1의 갯수 = j
    for (j--, n++; i !== j; i--) {
        n = n << 1; 
        } // 0자리에 1대입, 1의 갯수 -1, i === j 가 될때까지 죄로 쉬프트하면서 쉬프트 횟수 -1
    for (i; i; i--, n++) {
        n = n << 1; 
        } // i === 0 될때까지 좌로 쉬프트 하면서 쉬프트 횟수 -1, 0자리에 1대입
    return n;
}

올바른 괄호

해당 문제 링크

function solution(s){
    let stack = [];
    let split = s.split('')

    if (split[0] === ')') return false;

    console.log(split);
    console.log(stack);

    while(split.length > 0) {
        // 만약에 split[0]이 '(' 괄호라면 split에서 빼서 stack에 넣음
        if (split[0] === '(')
            stack.push(split.shift()); 
        // 만약에 split[0]이 ')'이고
        else {
            // stack에 '('가 있다면
            if (stack.includes('(')){
                stack.pop(); // 마지막으로 넣은 괄호를 빼고
                split.shift(); // split내에서도 하나 빼기
                console.log("stack", stack)
                console.log("split", split)
            } else {
                return false;
            }
        }
    }
    
    return stack.length > 0 ? false : true;
}

이 풀이는 효율성 테스트를 통과하지 못함
while문을 사용한 것이 문제였을까?

필터를 사용해보기로 했다

let split = s.split('')
   if (split[0] === ')') return false;
   let countLeft = split.filter(branket => branket === '(').length;
   let countRight = split.filter(branket => branket === ')').length;

   return countLeft === countRight ? true : false;

테스트 케이스를 통과하지 않는 경우가 있어 실패…

else if 케이스를 만들어서 가능한 수를 하나 더 고려해야 했음

function solution2_1(s) {
    let answer = true; 
    let left = 0; 
    let split = s.split('');

    for(let item of split) {
        if (item === '(') { // 왼쪽 괄호를 찾으면 left를 더해준다
            left++
        } else if (left > 0) { // 만약 '('가 아니라면 ')'일 것이고 그렇다면 left를 줄여준다
            left--
        } else { // 이 둘 다 아니라면 괄호의 짝이 없다는 뜻
            return false;
        }
    }

    answer = left === 0 ? true : false; // left가 0이 아니라면 false 일 것
    return answer;
}

Comment and share

21-03-17 알고리즘 문제풀기 및 노트 정리

Mar 17, 2021 in 알고리즘

기능개발

해당 문제 링크

앞에 있는 기능이 배포될 때 함께 배포된다 는 뜻이 선입선출식 자료구조를 사용하라는 뜻이었음

progresses와 speeds는 짝을 이루는 구조(같은 index값을 갖는 구조)

1. 한 번의 루프마다 progresses[index] + speeds[index]를 한다
    1-1. 만약 이때 값이 100을 넘었다면 해당 원소들을 각각 shift()한다
    1-2. cnt++과 더불어 index값을 줄여준다(원소를 뺐으므로)
    1-3. cnt값이 0이 아니라면 정답 배열에 넣어준다
2. 정답 배열을 리턴한다

function solution(progresses, speeds) {
    let answer = [];
    let cnt = 0; // 한번에 배포되는 기능 수

    while(progresses.length > 0) {
        progresses = progresses.map((el, index) => el + speeds[index]); 
        for (let i = 0, len = progresses.length; i < len; i++) {
            if(progresses[i] >= 100) {
                progresses.shift();
                speeds.shift();
                cnt++;
                i--;
            } else break;
        }

        if (cnt > 0) {
            answer.push(cnt); // 한번에 배포될 기능 수를 넣어줌
            cnt = 0; // 0으로 초기화
        }
    }
    return answer;
}

다른 방법

1 2	1. 각 기능마다 걸리는 시간을 소수점자리 올림으로 계산하여 배열을 만듦 2. 이 배열의 가장 처음값을 빼 변수로 저장하고 이 값을 기준으로 나머지

function solution(progresses, speeds) {
    let answer = [];
    let daysLeft = progresses.reduce((acc, cur, index) => {
        let day = Math.ceil((100-cur)/speeds[index]);
        acc.push(day);
        return acc;
    }, [])

    let func = daysLeft[0]
    let cnt = 1;
    for (let i = 1; i < daysLeft.length; i++) {
        if (func >= daysLeft[i]) 
            cnt++;
        else {
            answer.push(cnt);
            cnt = 1;
            func = daysLeft[i];
        }
        if (i === daysLeft.length-1)
            answer.push(cnt);
    }
    return answer;
}

이 방법은 작업 완료에 걸리는 일 수를 기준으로 배열을 돌며 배포할 기능 수를 push하는 방법

가장 큰 수

해당 문제 링크

처음에는 탐욕법으로 풀어야 하나 했는데 sort함수 하나로 해결 가능한 문제였음

테스트 케이스 11번이 0으로만 된 배열이 들어오므로 정수화(parseInt)해서 0이라면 “0”을 리턴하도록 해야 했음

function solution(numbers) {
    let answer = numbers.map(num => '' + num)
                            .sort((a,b) => (b+a) - (a+b))
                            .join('')
    return parseInt(answer,10) === 0 ? "0" : answer;
}

프린터

해당 문제 링크

1
2
3

1. 인쇄 대기목록의 가장 앞에 있는 문서(J)를 대기목록에서 꺼냅니다.
2. 나머지 인쇄 대기목록에서 J보다 중요도가 높은 문서가 한 개라도 존재하면 J를 대기목록의 가장 마지막에 넣습니다.
3. 그렇지 않으면 J를 인쇄합니다.

function solution(priorities, location) {
    let answer = 0;
    let queue = [...priorities]; // 프린트 큐에 깊은 복사
    let myPrint = location; 
    
    while (queue.length){ 
        // 프린트 큐 맨 처음 있는 작업보다 우선도가 더 크다면
        if (queue.some(priority => priority > queue[0])){
            // 첫 작업을 shift한 후 맨 마지막으로 push한다
            queue.push(queue.shift());
            if (myPrint === 0){
                myPrint += queue.length - 1;
            } else {
                // 인덱스 값은 0에서부터 시작되므로 -1 해주어야 함
                myPrint -= 1;
            }
        } else { 
        // 프린트 큐 맨 처음 작업이 제일 우선도가 높다면
            queue.shift(); // 해당 작업을 shift하고
            answer += 1; // 해답이 해당 작업임
            if (myPrint === 0){
                break;
            } else {
                myPrint -= 1;
            }
        }
    }
    return answer;
}

Comment and share

21-03-16 자바스크립트로 하는 자료구조와 알고리즘(11)

Mar 16, 2021 in 알고리즘, 서적

19장 동적 프로그래밍

동적 프로그래밍(이하 DP)은 문제를 더 작은 부분들로 쪼개는 과정이 포함된다
해시 테이블을 사용한다면 이미 계산된 피보나치 숫자를 저장할 수 있고 계산 없이 O(1)의 시간으로 그 값을 불러올 수 있기 때문에 더 빠르게 구현할 수 있다
1
2
3
4
5
6
let cache = {};
const fiboBest = n => {
if (n <= 1) return n;
if(cache[n]) return cache[n];
return (cache[n] = fiboBest(n-1) + fiboBest(n-2));
}
DP는 재계산을 피하기 위해 이미 계산된 값들을 저장하고 해당 값들을 사용하는 방법이다
- 중복 부분 문제 : DP에서 보통 문제의 해결책으로 해시 테이블과 배열, 행렬에 저장하는 방식을 사용하는데, 이 방식을 메모이제이션이라고 부른다
- 최적 부분 구조 : 문제의 부분 최적 해결책을 통해 큰 문제를 해결하는 방법
배낭 문제 알고리즘은 대표적인 DP의 예로 무게와 가치를 지니는 n개의 항목이 주어졌을 때 최대 w의 무게를 담을 수 있는 배낭에 가치의 최대값을 담는 문제
배열(배낭)에 담긴 n개의 항목이 최대값이 되려면
1. n번째 항목이 제외되는 경우: n-1개의 항목에서 얻은 최대값
2. n번째 항목을 포함하는 경우: n-1개의 항목에서 얻은 최대값 + n번째 항목의 값

동적 프로그래밍의 구현은 현재 배열 인덱스와 목표치를 객체에 대한 키로 사용해 결과를 저장함 (메모이제이션 활용)

const knapsackDP = (idx, weights, values, target, matrix) => {
  let result = 0;
  if(matrix[idx + '-' + target]) {
    return matrix[idx + '-' + target]
  }

  if(idx <= -1 || target <= 0) {
    result = 0
  } else if (weights[idx] > target) {
    result = knapsackDP(idx - 1, weights, values, target, matrix);
  } else {
    let current = knapsackDP(idx - 1, weights, values, target, matrix),
        currentPlusOther = values[idx] + knapsackDP(idx - 1, weights, values, target - weights[idx], matrix);
    result= Math.max(current, currentPlusOther);
  }
  matrix[idx + '-' + target] = result
  return result;
}

최장 공통 부분 수열 알고리즘
두 개의 수열이 있을 때 두 수열의 가장 긴 공통 부분 수열의 길이를 찾는 알고리즘
부분 수열 내 항목들이 연속일 필요는 없고 순서만 맞으면 됨

길이 m인 문자열 str1과 길이 n인 문자열 str2가 함수 LCS를 통해 최장 공통 부분을 구한다면

if (두 수열의 마지막 글자가 일치한다면) {
  result = 1 + LCS(X[0:m-2], Y[0:n-2])
}
if (두 수열의 마지막 글자가 일치하지 않는다면) {
  result = Math.max(LCS(X[0:m-1], Y[0:n-1]), LCS(X[0:m-2], Y[0:n-2]))
}

재귀를 기반으로 의사 코드를 구현

const LCSNaive = (str1, str2, str1Length, str2Length) => {
  if (str1Length === 0 || str2Length === 0) {
    return 0;
  }

  if (str1[str1Length-1] === str2[str2Length-1]) {
    return 1 + LCSNavie(str1, str2, str1Length - 1, str2Length - 1);
  } else {
    return Math.max(
      LCSNavie(str1, str2, str1Length, str2Length - 1),
      LCSNavie(str1, str2, str1Length - 1, str2Length)
      )
  }
}

const LCSNaiveWrapper = (str1, str2) => {
  return LCSNaive(str1, str2, str1.length, str2.length);
}

DP식 접근법

const longestCommonSequenceLength = (str1, str2) => {
  let matrix = Array(str.length + 1).fill(Array(str2.length + 1).fill(0)), 
      rowLength = str1.length + 1,
      colLength = str2.length + 1,
      max = 0;
  for (let row = 1; row < rowLength; row++) {
    for (let col = 1; col < colLength; col++) {
      let str1Char = str1.charAt(row - 1),
          str2Char = str2.charAt(col - 1);
      
      if (str1Char === str2Char) {
        matrix[row][col] = matrix[row - 1][col - 1] + 1;
        max = Math.max(matrix[row][col], max);
      }
    }
  }
  return max;
}

동전 교환 알고리즘 : 동전의 금액 종류 M개가 들어있는 객체 S가 주어질때 금액 n을 동전으로 교환하기 위한 조합을 구하는 문제

이때 이 문제의 최적 부분 구조는 (1) M번째 동전이 포함되지 않는 해결책과 (2) M번째 동전이 최소 한 개 포함되는 해결책 으로 나눌 수 있다
coinChange(S, M, n) = coinChange(S, M-1, N) + coinChanges(S, M, N-Sm)

// coinArr의 인덱스는 [0, ..., coinIndex]
const countCoinWays = (coinArr, coinIndex, total) => {
  if (total === 0) return 1;
  // total 값이 0에 도달한 경우에는 아무 동전도 포함하지 않는 것
  if (total < 0 || (coinIndex <= 0 && total >= 1)) return 0;
  // total값이 0 보다 작다는 것은 M번째 동전이 포함되거나 포함되지 않을 때의 해결책이 없다는 뜻
  // 남은 동전이 없을 때 (index값은 coinArr.length에서 점점 줄어드므로) total값을 채우지 못해도 해결책이 없다는 뜻

  return countCoinWays(coinArr, coinIndex - 1, total) +
        countCoinWays(coinArr, coinIndex - 1, total - coinArr[coinIndex - 1])
}
const countCoinWaysWrapper = (coinArr, total) => {
  return countCoinWays(coinArr, coinArr.length, total);
}

하지만 이 방법을 사용한다면 중복 부분 문제가 많다

동전 교환 알고리즘을 DP로 구현하기

const countCoinWaysDP = (coinArr, coinIndex, total) => {
  let dpMatrix = [];
  // 메모이제이션용 행렬, 추후 2차원 배열이 된다
  for (let i = 0; i <= total; i++) {
    dpMatrix[i] = [];
    // 원하는 값까지 전부 배열이 들어가게 된다
    for (let j = 0; j < coinIndex; j++) {
      dpMatrix[i][j] = undefined;
      // undefined로 초기화
    }
  }

  for (let i = 0; i < coinIndex; i++) {
    // 맨 윗줄을 1로 채움 (undefined에서 기본값으로)
    dpMatrix[0][i] = 1;
  }

  for (let i = 1; i < total + 1; i++) {
    // 행렬의 세로이동
    for (let j = 0; j < coinIndex; j++) {
      // 행렬의 가로이동
      let temp1 = 0, temp2 = 0;
      // 두 가지의 부분 방법으로 나뉘므로 temp값도 두개가 필요함
      if (i - coinArr[j] >= 0) {
        temp1 = dpMatrix[i - coinArr[j]][j];
        // temp1값에 dpMatrix[0][0] 번값부터 가로줄 값을 저장
      }

      if (j >= 1) {
        temp2 = dpMatrix[i][j-1];
        // temp2값에 dpMatrix[1][0] 값부터  세로줄 값을 저장
      }
      
      // dpMatrix[1][0] 값부터 temp1(M번째 동전이 포함되지 않는 해결책)값과 
      // temp2(M번째 동전이 최소한 한 개 포함되는 해결책)값을 더해 저장
      dpMatrix[i][j] = temp1 + temp2;
    }
  }

  // 결과값이 저장되어있는 것 중에서 total값을 만족하는 행의 max값을 리턴함 
  // if()에서도 i < coinIndex 와 같이 리턴하였으므로 여기서도 -1 해주어야 함
  return dpMatrix[total][coinIndex - 1]
}

const countCoinWaysDPWrapper = (coinArr, coinValue) => {
  return countCoinWaysDP(coinArr, coinArr.length, coinValue);
}

편집 거리 알고리즘 (레벤슈타인 거리 알고리즘)

길이 m인 문자열 str1과 길이 n인 문자열 str2가 주어졌을때 str1을 str2로 변환하기 위환 최소 편집 횟수는? (이 때, 사용가능한 연산은 삽입, 제거, 교환만 가능하다)

if (문자가 동일하다)
  아무것도하지 않는다
if (문자가 다르다) {
  1) m과 n-1의 삽입
  2) m-1과 n의 제거
  3) m-1과 n-1의 교환 
  세가지를 재귀적으로 고려
}

Brute-force 방법으로 구현하기

const editDistanceRecursive = (str1, str2, length1, length2) => {
  // 빈문자열이라면 나머지 한 쪽의 문자열을 그대로 복사하면 되므로 나머지 한 쪽 길이값을 리턴함 (length1 or length2번 시행해야 하므로)
  if (length1 === 0) return length2;
  if (length2 === 0) return length1;

  // 마지막 글자가 같다면 마지막 글자를 제외한 나머지 문자만큼 돌면 된다
  // 이 과정은 재귀적으로 반복되므로 맨 마지막 글자부터 첫번째 글자까지 비교를 할 것
  if (str[length1-1] === str2[length2-1]) 
    return editDistanceRecursive(str1, str2, length1-1, length2-1)

  return 1 + Math.min(
    editDistanceRecursive(str1, str2, length1, length2-1), // 삽입
    editDistanceRecursive(str1, str2, length1-1, length2), // 제거
    editDistanceRecursive(str1, str2, length1-1, length2-1) // 교환
  )
}

const editDistanceRecursiveWrapper = (str1, str2) => {
  return editDistanceRecursive(str1, str2, str1.length, str2.length)
}

DP식 접근법

const editDistanceDP = (str1, str2, length1 = str1.length, length2 = str2.length2) => {
  let dpMatrix = [];
  for (let i = 0; i < length1+1; i++) {
    dpMatrix[i] = [];
    for (let j = 0; j < length2+1; j++) {
      dpMatrix[i][j] = undefined;
    }
  }
  // let dpMatrix = Array.from({length: length1+1}, 
  //           () => Array.from({length:length2+1}, () => undefined))

  for (let i = 0; i < length+1; i++) {
    for (let j = 0; j < length2+1; j++) {
      if (i === 0) {
        dpMatrix[i][j] = j;
      } else if (j === 0) {
        dpMatrix[i][j] = i;
      } else if (str1[i-1] === str2[j-1]) {
        dpMatrix[i][j] = dpMatrix[i-1][j-1];
      } else {
        let insertCost = dpMatrix[i][j-1],
            removeCost = dpMatrix[i-1][j],
            replaceCost = dpMatrix[i-1][j-1];

        dpMatrix[i][j] = 1 + Math.min(insertCost, removeCost, replaceCost)
      }
    }
  }
  return dpMatrix[length1][length2];
}

20장 비트 조작

고성능 서버 사이드 코드를 구현하길 원한다면 비트 조작도 알아야 함
자바스크립트의 비트 연산자
&는 AND, |는 OR, ~는 NOT, ^는 XOR에 해당하고 왼쪽 이동은 <<로, 오른쪽 이동은 >>로, >>>는 오른쪽 이동 후에 0으로 채운다는 뜻이다
AND 연산자(&)는 두 개의 비트가 모두 1일때 참이다
a = 1100, b = 1010일 때, a & b = 1000이다
OR 연산자(|)는 두 개의 비트 중 하나만 1이어도 참이다
a = 1100, b = 1010일 때, a & b = 1110이다
XOR 연산자(^)는 비트 중 하나가 1일 때만 참이 된다
a = 1100, b = 1010일 때, a & b = 0110이다
NOT 연산자는 모든 비트를 뒤집는다
a = 1100일 때 NOT a = 0011이다
왼쪽 이동 연산자(<<)는 모든 비트가 왼쪽으로 이동되고 왼쪽 끝 범위를 벗어나는 비트는 버려진다
9(1001) << 1 = 10010(2) = 18, 9 << 2 = 100100(2) = 36
위 예와 같이 왼쪽 이동 연산자는 해당 항목을 두 배로 증가시킨다 (이진 연산 체계이기 때문) 하지만 왼쪽 이동으로 비트가 넘친다면 버려지므로 값이 작아질 수 있다
오른쪽 이동 연산자(>>)는 모든 비트가 오른쪽으로 이동되고 오른쪽 끝 범위를 벗어나면 버려진다
9(1001) >> 1 = 100(2) = 4
오른쪽 이동 연산자는 항목을 2로 나눈 값이 된다

비트 연산자를 사용해 연산해보기

// 이진수를 더하기는  두 수를 더한 다음 10을 초과하면 1을 다음 수로 올린다 (carry)
const BitwiseAdd = (a, b) => {
  while (b !== 0) {
    let carry = (a & b);
    a = a ^ b;
    b = carray << 1;
  }
  return a;
}

// 이진수에서 음의 이진수로부터 양의 이진수를 빼려면 모든 비트를 뒤집은 다음 1을 더하면 된다
const BitwiseNegate = a => {
  return BitwiseAdd(~a, 1);
}

// 빼기는 음수를 더하는 것이기 때문에 음의 이진수를 구하고 더한다
const BitwiseSubtract = (a, b) => {
  return BitwiseAdd(a, BitwiseNegate(b))
}

// 곱셈은 두 수를 곱하고 10이 넘어가는 수는 다음 자릿수로 올리고 다음 자릿수로 이동해 해당 자릿수의 수를 곱한다
const BitwiseMultiply = (a, b) => {
  let m = 1, c = 0;
  if (a < 0) {
    a = BitwiseNegate(a);
    b = BitwiseNegate(b);
  }

  while (a >= m && b) {
    if (a & m) 
      c = BitwiseAdd(b, c);
    b = b << 1;
    m = m << 1;
  }
  return c;
}

// a나누기 b는 b를 여러번 빼는 것이라고 생각하면 쉽다
const BitwiseDividePositive = (a, b) => {
  let c = 0;
  if (b !== 0) {
    while (a >= b) {
      a = BitwiseSubtract(a, b);
      c++
    }
  }
  return c;
}

// 하지만 음의 정수를 나누기한다면 while값이 무한히 반복될 것이기 때문에 부호를 저장할 값이 필요하다
const BitwiseDivide = (a, b) => {
  let c = 0, isNegative = 0;

  if (a < 0) {
    a = BitwiseNegate(a);
    isNegative = !isNegative;
  }

  if (b < 0) {
    b = BitwiseNegate(b);
    isNegative = !isNegative;
  }

  if (b !== 0) {
    while (a >= b) {
      a = bitwiseSubstract(a, b);
      c++;
    }
  }

  if (isNegative) {
    c = BitwiseNegate(c);
  }
  return c;
}

비트연산자는 Math의 기본 함수보다 빠르다
최근의 자바스크립트는 Node.js를 활용해 서버 측 프로그래밍에 진입하고 있기 때문에 비트 연산자는 효율적인 코드를 만드는데 도움이 될 것이다

Comment and share

21-03-15 자바스크립트로 하는 자료구조와 알고리즘(10)

Mar 15, 2021 in 알고리즘, 서적

18장 고급 문자열

트라이(trie)는 문자열을 검색해 저장된 문자열 중 일치하는 문자열이 있는지 확인하는데 주로 사용되는 특별한 종류의 트리

트라이는 중첩 객체를 사용해 구현되는데 각 노드는 자신과 직접 연결된 자식들을 지니고 이 자식들은 키 역할을 한다

class TrieNode {
  constructor() {
    this.children = {};
    this.endOfWord = false;
  }
}

class Trie {
  constructor() {
    this.root = new TrieNode(); // 생성되면 하나의 트라이 노드를 갖는다
  }

  insert(word) {
    let current = this.root; // 현재 노드값을 가져옴 이 노드에는 children 객체와 endOfWord가 존재함
    for (let i = 0, len = word.length; i < len; i++){
      let ch = word.charAt(i);
      let node = current.children[ch]; // 객체(children{})내 항목 참조
      if (node === null) {
        node = new TrieNode();
        current.children[ch] = node;
      }
      current = node;
    }
    current.endOfWord = true;
  }

  search(word) {
    let current = this.root;
    for (let i = 0, len = word.length; i < len; i++) {
      let ch = word.charAt(i);
      let node = current.children[ch]; 
      if (node === null) {
        return false;
      }
      current = node;
    }
    return current.endOfWord;
  }

  delete(word) {
    this.deleteRecursively(this.root, word, 0);
  }

  deleteRecursively(current, word, index) {
    if (index === word.length) {
      if (!current.endOfWord) return false
      current.endOfWord = false;
      return Object.keys(current.children).length === 0;
    }
    let ch = word.charAt(index),
        node = current.children[ch];
    
    if (node === null) return false;
    let shouldDeleteCurrentNode = this.deleteRecursively(node, word, index+1); 
    // shouldDeleteCurrentNode의 리턴은 boolean값이므로 이 값이 true라면 삭제해야 한다

    if(shouldDeleteCurrentNode) {
      delete current.children[ch];
      return Object.keys(current.children).length === 0;
    }
    return false
  }
}

보이어-무어 문자열 검색

텍스트 편집기 어플리케이션과 웹 브라우저의 ‘찾기’기능에 사용됨

const buildBadMatchTable = str => {
  let tableObj = {},
      strLength = str.length;
  for (let i = 0; i < strLength - 1; i++) {
    tableObj[str[i]] = strLength - 1 - i;
  }
  if (tableObj[str[strLength-1]] === undefined) {
    tableObj[str[strLength-1]] = strLength;
  }
  return tableObj;
}

보이어-무어 문자열 검색 알고리즘의 구현
패턴으로 사용할 문자열을 입력받을 때 검색하고자 하는 현재 문자열이 불일치 표에 존재하면 인덱스를 건너 뛴다

현재 문자열이 불일치 표에 존재하지 않다면 인덱스를 1 증가시킴

const boyerMoore = (str, pattern) => {
  let badMatchTable = buildBadMatchTable(pattern),
      offset = 0,
      patternLastIndex = pattern.length - 1,
      scanIndex = patternLastIndex,
      maxOffset = str.length - pattern.length;
  while (offset <= maxOffset) {
    scanIndex = 0;
    while (pattern[scanIndex] === str[scanIndex + offset]) {
      if (scanIndex === patternLastIndex) {
        return offset;
      }
      scanIndex++;
    }
    let badMatchString = str[offset + patternLastIndex];
    if (badMatchTable[badMatchString]) {
      offset += badMatchTable[badMatchString]
    } else {
      offset += 1;
    }
  }
  return -1;
}

보이어-무어 알고리즘은 최선의 경우 모든 문자가 동일할 때이고 이 때의 시간 복잡도는 O(W/T)이다 (이때, W는 패턴을 찾고자 하는 대상인 문자열)
최악의 경우 패턴이 문자열의 끝에 존재하고 앞부분이 모두 고유의 문자로 구성된 경우고 이 때의 시간 복잡도는 O(T*W)가 된다
이보다 조금 더 빠른 구현을 위해서는 커누스-모리스-플랫 문자열 검색 알고리즘(이후 KMP 알고리즘)을 사용할 수 있다
KMP 알고리즘은 입력 텍스트 T 내에서 단어 W의 출현 횟수를 검색한다
접두사 배열을 만들 때 접두사 배열이 동일한 접두사를 얻기 위해 인덱스를 얼마나 되돌려야 할지를 나타낼 수 있도록 해야 한다

접두사 표 만들고 KMP 검색

const longestPrefix = str => {
  let prefix = new Array(str.length);
  let maxPrefix = 0;
  prefix[0] = 0;
  for (let i = 1, len = str.length; i < len; i++) {
    while (str.charAt(i) !== str.charAt(maxPrefix) && maxPrefix > 0) {
      maxPrefix = prefix[maxPrefix - 1];
    }
    if (str.charAt(maxPrefix) === str.charAt(i)) {
      maxPrefix++;
    }
    prefix[i] = maxPrefix;
  }
  return prefix;
}

const KMP = (str, pattern) => {
  let prefixTable = longestPrefix(pattern),
      patternIndex = 0,
      strIndex = 0;
  while (strIndex < str.length) {
    if (str.charAt(strIndex) !== pattern.charAt(patternIndex)) {
      if (patternIndex !== 0) {
        patternIndex = prefixTable[patternIndex - 1];
      } else {
        strIndex++;
      }
    } else if (str.charAt(strIndex) === pattern.charAt(patternIndex)) {
      strIndex++;
      patternIndex++;
    }

    if (patternIndex === pattern.length) {
      return true;
    }
  }
  return false;
} // 시간 복잡도는 O(W)

라빈-카프 검색 알고리즘은 텍스트에서 특정 패턴을 찾기 위해 해싱을 활용한다
해시 함수(라빈 지문 해싱 기법)를 통해 부분 문자열이 패턴과 동일한지 비교하는 과정의 속도를 높인다
라빈 지문

라빈 지문을 이용한 해시 함수

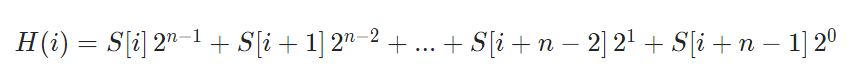
class RabinKarpSearch {
  constructor () {
    this.prime = 101;
  }

  rabinkarpFingerprintHash (str, endLength) {
    if (endLength === null) endLength = str.length;
    let hashInt = 0;
    for (let i = 0; i < endLength; i++) {
      hashInt += str.charCodeAt(i) * Math.pow(this.prime, i);
    }
    return hashInt;
  }

  recalculate (str, oldIndex, newIndex, oldHash, patternLength) {
    if (patternLength === null) patternLength = str.length;
    let newHash = oldHash - str.charCodeAt(oldIndex);
    newHash = Math.floor(newHash/this.prime);
    newHash += str.charCodeAt(newIndex) * Math.pow(this.prime, patternLength - 1);
    return newHash;
  }

  strEquals (str1, startIndex1, endIndex1, str2, startIndex2, endIndex2) {
    if(endIndex1 - startIndex1 !== endIndex2 - startIndex2) return false;
    while (startIndex1 <= endIndex1 && startIndex2 <= endIndex2) {
      if (str1[startIndex] !== start2[startIndex2]) {
        return false;
      }
      startIndex1++;
      startIndex2++;
    }
    return true;
  }

  rabinkarpSearch (str, pattern) {
    let T = str.length,
        W = pattern.length,
        patternHash = this.rabinkarpFingerprintHash(pattern, W),
        textHash = this.rabinkarpFingerprintHash(str, W);

    for (let i = 1; i <= T - W + 1; i++) {
                                        // strEquals (str1, startIndex1, endIndex1, str2, startIndex2, endIndex2) 
      if (patternHash === textHash && this.strEquals(str, i - 1, i + W - 2, pattern, 0, W - 1)) {
        return i - 1;
      }
      if (i < T - W + 1) {
                    // recalculate (str, oldIndex, newIndex, oldHash, patternLength)
        textHash = this.recalculateHash(str, i - 1, i + W - 1, textHash, null);
      }
    }
    return -1;
  }
}

라빈-카프 알고리즘은 원본 자료가 있는 경우 표절 검사 등에 사용될 수 있다

Comment and share

21-03-14 자바스크립트로 하는 자료구조와 알고리즘(9)

Mar 14, 2021 in 알고리즘, 서적

16장 힙

힙은 O(1) 시간으로 가장 높은 항목이나 가장 낮은 항목을 반환하는 중요한 자료 구조
힙은 트리와 비슷한 자료 구조의 일종으로 최대 힙의 경우 부모가 자식보다 크고 최소 힙의 경우 부모가 자식보다 작다
힙은 자식에 대한 포인터를 갖는 대신에 배열을 사용해 자료를 저장함
배열을 사용하므로 인덱스를 통해 힙 노드의 자식 위치를 쉽게 계산할 수 있다
힙이 배열을 사용해 자료를 저장하기 때문에 인덱스는 각 항목의 차수/높이를 정의 한다
첫 번째 배열 항목을 루트로 설정하고 각 왼쪽 항목과 오른쪽 항목을 순서대로 채워 이진 힙을 만들 수 있다

최대 힙은 루트노드가 가장 높은 값을 갖고 최소 힙은 루트노드가 가장 낮은 값을 갖는다

class Heap {
    // 힙은 배열을 사용해 자료를 저장
    constructor () {
        this.items = [];
    }

    // 두 개의 인덱스에 위치한 값을 바꾸는 것도 인덱스 값으로 변경 가능함
    swap(idx1, idx2) {
        let temp = this.itmes[idx1];
        this.itmes[idx1] = this.items[idx2];
        this.items[idx2] = temp;
    } 

    parentIndex(idx) {
        return Math.floor((idx-1)/2);
    }

    leftChildIndex(idx) {
        return index * 2 + 1;
    }

    rightChildIndex(idx) {
        return idx * 2 + 2;
    }

    parent(idx) {
        return this.items[this.parentIndex(idx)];
    }

    leftChild(idx) {
        return this.items[this.leftChildIndex(idx)];
    }

    rightChild(idx) {
        return this.items[this.rightChildIndex(idx)];
    }

    peek(item) {
        return this.items[0];
    }

    size() {
        return this.items.length;
    }
}

예를들어 최소 힙 구조인 배열이 [2, 4, 23, 12, 13] 라면 부모 노드인 0번 인덱스 2가 부모가 될 것이고 1번 인덱스인 4는 왼쪽 자식이, 2번 인덱스인 23은 오른쪽 자식이 된다
항상 좌측이 먼저 채워지고 우측이 채워지므로 3번 인덱스는 1번 인덱스의 왼쪽 자식이 되고 4번 인덱스는 1번 인덱스의 오른쪽 자식이 된다
정리하면 자신의 인덱스가 N이라고 한다면 부모는 (N - 1)/2 의 인덱스를 가질 것이고(예를 들어 N = 3 일 때, 부모의 인덱스는 1), 왼쪽 자식은 (N * 2) + 1 의 인덱스를, 힙 배열이 순차적이라면 오른쪽 자식은 바로 옆에 붙어있어야 하므로 (N * 2) + 2 의 인덱스를 가질 것이다

항목을 추가하거나 삭제하더라도 힙의 구조가 유지되어야 한다

class MinHeap extends Heap{
    constructor () {
        super();
        this.items = [];
    }

    add(item) {
        this.items[this.items.length] = item;
        this.bubbleUp();
    }

    poll() {
        let item = this.items[0];
        this.items[0] = this.items[this.items.length - 1];
        this.items.pop();
        this.bubbleDown();
        return item;
    }

    bubbleDown() {
        let index = 0;
        while (this.leftChild(index) && this.leftChild(index) < this.items[index]) {
            let smallerIndex = this.leftChildIndex(index);
            if (this.rightChild(index) && this.rightChild(index) < this.items[smallerIndex])
                smallerIndex = this.rightChildrenIndex(index);  
            this.swap(smallerIndex, index);
            index = smallerIndex;
        }
    }

    bubbleUp() {
        let index = this.items.length - 1;
        while(this.parent(index) && this.parent(index) > this.items[index]) {
            this.swap(this.parentIndeX(index), index);
            index = this.parentIndex(index);
        }
    }
}

최대 힙의 경우 최소 힙에서 구현한 bubbleDown과 bubbleUp 내 비교자 뿐이다

bubbleDown() {
    let index = 0;
    while (this.leftChild(index) && this.leftChild(index) > this.items[index]
            || this.rightChild(index) > this.items[index]) {
        let biggerIndex = this.leftChildIndex(index);
        if (this.rightChild(index) && this.rightChild(index) < this.items[biggerIndex])
            biggerIndex = this.rightChildrenIndex(index);  
        this.swap(biggerIndex, index);
        index = biggerIndex;
    }
}

bubbleUp() {
    let index = this.items.length - 1;
    while(this.parent(index) && this.parent(index) < this.items[index]) {
        this.swap(this.parentIndeX(index), index);
        index = this.parentIndex(index);
    }
}

힙 노드 인덱스 요약

노드	인덱스
자신	N
부모	(N - 1) / 2
왼쪽 자식	(N * 2) + 1
오른쪽 자식	(N * 2) + 2

힙은 삼투를 통해 자신의 구조를 유지한다(bubbleUp, bubbleDown)
이 삼투 과정이 있어 삭제와 삽입이 O(log2(n)) 시간에 가능해진다

일련의 숫자에서 중간 값을 찾기

/*
    하나의 최소 힙과 하나의 최대 힙을 만들면 중간 값을 얻는 데 O(1)시간이 걸림
*/

class MedianHeap {
    constructor() {
        this.minHeap = new MinHeap();
        this.maxHeap = new MaxHeap();
    }

    add(value) {
        if (value > this.median()) 
            this.minHeap.add(value);
        else 
            this.maxHeap.add(value);
        

        if (this.minHeap.size() - this.maxHeap.size() > 1) 
            this.maxHeap.add(this.minHeap.poll());
        
        if (this.maxHeap.size() - this.minHeap.size() > 1)
            this.minHeap.add(this.maxHeap.poll());
    }

    median() {
        if(this.minHeap.size() === 0 && this.maxHeap.size() === 0) 
            return Number.NEGATIVE_INFINITY;
        else if (this.minHeap.size() === this.maxHeap.size())
            return (this.minHeap.peek() + this.maxHeap.peek()) / 2;
        else if (this.minHeap.size() > this.maxHeap.size()) 
            return this.minHeap.peek();
        else 
            return this.maxHeap.peek();
    }
}

배열에서 K번째로 가장 작은/큰 값 찾기

let arr = [12, 3, 13, 4 ,2, 40, 23];
const getKthSmallestElement = (arr, k) => {
    let minH = new MinHeap();
    for (let i = 0, len = arr.length; i < len; i++) {
        minH.add(arr[i]);
    }
    
    for (let i = 1; i < k; i++) {
        minH.poll();
    }

    return minH.poll();
}

const getKthSmallestElement = (arr, k) => {
    let maxH = new MaxHeap();
    for (let i = 0, len = arr.length; i < len; i++) {
        maxH.add(arr[i]);
    }
    
    for (let i = 1; i < k; i++) {
        maxH.poll();
    }

    return maxH.poll();
}

17장 그래프

그래프를 사용하면 객체 간의 연결을 다양하게 나타낼 수 있다
그래프 기본 용어 및 개념

단어	뜻
정점	그래프를 형성하는 노드로 원으로 표기
간선	그래프에서 노드 간의 연결로 정점(원)사이의 선으로 표기
정점 차수	해당 점점에 연결된 간선의 개수
희소 그래프	정점들 간 가능한 연결 중 일부만 존재하는 경우
밀집 그래프	다양한 정점들 간에 연결이 많은 경우
순환 그래프	어떤 정점에서 출발해 해당 정점으로 다시 돌아오는 경로가 있는 지향성 그래프
가중치	간선에 대한 값으로 문맥에 따라 다양한 것을 나타냄(정점 간 거리 등)

무지향성 그래프는 간선 간에 방향이 없는 그래프로 노드 간 방향 없이 상호 연결을 뜻한다
인접 행렬과 인접 리스트를 사용하여 무지향성 그래프를 자료 구조 클래스로 표현할 수 있다

가중치가 있는 무지향성 그래프에 정점과 간선을 추가하기

class UndirectedGraph {
    constructor () {
        this.edges = {};
    }

    addVertext(vertex) {
        this.edges[vertex] = {};
    }

    addEdge(vertex1, vertex2, weight) {
        if (weight === undefined)
            weight = 0;
        this.edges[vertex1][vertex2] = weight;
        this.edges[vertex2][vertex1] = weight;
    }

    removeEdge(vertex1, vertex2) {
        if (this.edges[vertex1] && this.edges[vertex1][vertex2] !== undefined) 
            delete this.edges[vertex1][vertex2]
        if (this.edges[vertex2] && this.edges[vertex2][vertex1] !== undefined)
            delete this.deges[vertex2][vertex1]
    }

    removeVertex = function(vertex) {
        for (let adjacentVertex in this.edges[vertex]) {
            this.removeEdge(adjacentVertex, vertex);
        }
        delete this.edges[vertex];
    }
}

정점간에 방향이 있는 지향성 그래프를 구현하기

class DirectedGraph {
    constructor() {
        this.edges = {};
    }

    addVertex(vertex) {
        this.edges[vertex] = {};
    }

    addEdge(origVertex, destVertex, weight) {
        if(weight === undefined)
            weight = 0;

        this.edges[origVertex][destVertex] = weight;
    }

    removeEdge(origVertex, destVertex) {
        if(this.edges[origVertex] && this.edges[origVertex][destVertex] !== undefined)
            delete this.deges[origVertex][destVertex];
    }

    removeVertex(vertex) {
        for (let adjacentVertex in this.edges[vertex])
            this.removeEdge(adjacentVertex, vertex);
        delete this.edges[vertex];
    }

    traverseBFS(vertex, fn) {
        let queue = [], visited = {};
        queue.push(vertex);

        while(queue.length) {
            vertex = queue.shift();
            if(!visited[vertex]) {
                visited[vertex] = true;
                fn(vertex);
                for (let adjacentVertex in this.edges[vertex]) {
                    queue.push(adjacentVertex);
                }
            }
        }
    }

    traverseDFS(vertex, fn) {
        let visited = {};
        this._traverseDFS(vertex, visited, fn);
    }

    _traverseDFS(vertex, visited, fn) {
        visited[vertex] = true;
        fn(vertex);
        for (let adjacentVertex in this.edges[vertex]) {
            if(!visited[adjacentVertex])
                this. _traverseDFS(adjacentVertex, visited, fn)
        }
    }
}

가중치가 있는 그래프와 최단 경로
다익스트라 알고리즘은 목적지에 도달하기 위해 각 단계에서 최단 경로를 취하는 방식으로 동작한다

처음에는 일부 노드에 도달할 수 없을 수도 있기 때문에 거리를 무한으로 표기한다

function _isEmpty(obj) {
    return Object.keys(obj).length === 0;
}

function _extractMin(Q, dist) {
    let minimumDistance = Infinity,
        nodeWithMinimumDistance = null;
    for (let node in Q) {
        if (dist[node] <= minimumDistance) {
            minimumDistance = dist[node];
            nodeWithMinimumDistance = node;
        }
    }
    return nodeWithMinimumDistance;
}
// class DirectedGraph 내부라고 가정
    Dijkstra(source) {
        let Q = {}, dist = {};
        for (let vertex in this.edges) {
            dist[vertex] = Infinity;
            Q[vertex] = this.edges[vertex];
        }
        dist[source] = 0;

        while (!_isEmpty(Q)) {
            let u = _extractMin(Q, dist);
            delete Q[u];

            for (var neighbor in this.edges[u]){
                let alt = dist[u] + this.edges[u][neighbor];
                if (alt < dist[neighbor]) 
                    dist[neighbor] = alt;
            }
        }
        return dist;
    }

위상 정렬 알고리즘은 순서를 기록하기 위해 스택을 사용하는 수정된 버전의 깊이 우선 정렬

이 알고리즘은 어떤 노드로부터 깊이 우선 정렬을 수행해 해당 노드와 연결된 모든 노드들을 재귀적으로 방문하면서 해당 노드들을 스택에 추가한다

// class DirectedGraph 내부라고 가정
    topologicalSortUtil(v, visited, stack) {
        visited.add(v);
        for (let item in this.edges[v]){
            if (visited.has(item) === false) {
                this.topologicalSortUtil(item, visited, stack)
            }
        }
        stack.unshift(v);
    }

    topologicalSort() {
        let visited = new Set(), stack = [];

        for (let item in this.edges) {
            if (visited.has(item) === false) {
                this.topologicalSortUtil(item, visited, stack);
            }
        }
        return stack;
    }

Comment and share

21-03-13 자바스크립트로 하는 자료구조와 알고리즘(8)

Mar 13, 2021 in 알고리즘, 서적

15장 트리

이진 트리는 자식 노드가 왼쪽과 오른쪽뿐인 트리이다

class BinaryTreeNode {
  constructor (value) {
    this.value = value;
    this.left = null;
    this.right = null;
  }
}

class BinaryTree {
  this._root = null;
}

트리를 순회하려면 인덱스를 사용해 트리에 접근한 다음 크기 제한에 도달할 때까지 인덱스를 증가한다

선순위, 후순위, 중순위, 단계순위 순회 등이 있다

// 선순위
  traversePreOrder () {
    traversePreOrderHelper(this._root);

    function traversePreOrderHelper(node) {
      if(!node) return;
      console.log(node.value);
      traversePreOrderHelper(node.left);
      traversePreOrderHelper(node.right);
    }
  }

  traversePreOrderInterative() {
    let nodeStack = [];
    nodeStack.push(this._root);

    /*
    1) 항목을 출력
    2) 오른쪽 자식을 스택에 추가
    3) 왼쪽 자식을 스택에 추가
    스택구조이므로 오른쪽을 먼저 넣고 왼쪽을 나중에 넣음 (pop으로 꺼내면 왼쪽이 먼저 처리됨)
    */
    while (nodeStack.length) {
      let node = nodeStack.pop();
      console.log(node.value);
      if(node.right) nodeStack.push(node.right);
      if(node.left) nodeStack.push(node.left);
    }
  }

// 중순위
  traverseInOrder() {
    traverseInOrderHelper(this._root);

    function traverseInorderHelper(node) {
      if(!node) return;
      traverseInOrderHelper(node.left);
      console.log(node.value);
      traverseInOrderHelper(node.right);
    }
  }

  traverseInOrderInterative() {
    let current = this._root,
        s = [],
        done = false;
    
    while (!done) {
      // 현재 노드의 가장 왼쪽에 있는 노드로 이동
      if (current != null) {
        // 왼쪽 하위 트리를 순회하기 전에 포인터가 스택의 트리 노드를 가리키도록 함
        s.push(current);
        current = current.left
      } else {
        if(s.length) {
          current = s.pop();
          console.log(current.value);
          current = current.right;
        } else {
          done = true;
        }
      }
    }
  }

// 후순위
  traversePostOrder() {
    traversePostOrderHelper(this._root);

    function traversePostOrderHelper(node) {
      if (node.left) 
        traversePostOrderHelper(node.left)
      if (node.right)
        traversePostOrderHelper(node.right)
      console.log(node.value);
    }
  }

  traversePostOrderInterative() {
    let s1 = [], s2 = [];
    s1.push(this._root);
    while(s1.length) {
      let node = s1.pop();
      s2.push(node)

      if (node.left) 
        s1.push(node.left);
      if (node.right) 
        s1.push(node.right);
    }
    while(s2.length) {
      let node = s2.pop();
      console.log(node.value);
    }
  }
// 단계순위 순회
  traverseLevelOrder() {
    let root = this._root, queue = [];
    if(!root) return;
    queue.push(root);
    
    while(queue.length) {
      let temp = queue.shift();
      console.log(temp.value);
      if(temp.left) queue.push(temp.left);
      if(temp.right) queue.push(temp.right);
    }
  }

리프 노드를 방문하기 전에 루트를 조사할 필요가 있는 경우 선순위 순회 를 선택
리프 노드를 검색할 때 루트를 조사하느라 시간을 낭비하기 싫다면 후순위 순회 를 선택
트리를 원래 순서대로 방문하고 싶은 경우에는 중순위 순회 를 선택
이진 검색 트리의 경우 왼쪽 자식이 부모보다 작고 오른쪽 자식이 부모보다 크다

자식이 부모 값보다 큰 노드만 있는 경우 불균형 이진 검색트리가 되고 이 트리는 완전 균형 이진 트리에 비해 복잡도가 O(log2n)에서 O(n)으로 늘어난다

class BinarySearchTree {
  constructor () {
    this._root = null;
  }

  insert(value) {
    let thisNode = { left : null, right : null, value: value};
    if (!this._root) {
      this._root = thisNode;
    } else {
      let curRoot = this._root;
      while(true) {
        if (curRoot.value > value) {
          // 현재 노드보다 값이 작다면 왼쪽에 삽입
          if (curRoot.left != null) {
            curRoot = curRoot.left;
          } else {
            curRoot.left = thisNode;
            break;
          }
        } else if (curRoot.value < value) {
          // 현재 노드보다 값이 크면 오른쪽에 삽입
          if (curRoot.right != null) {
            curRoot = curRoot.right;
          } else {
            curRoot.right = thisNode;
            break;
          }
        } else {
          // 현재 노드와 값이 같을 경우
         break; 
        }
      } 
    }
  } // insert() end

  /*
    삭제하고자 하는 노드를 찾기 위해 트리를 순회해야 한다
    노드에 자식이 없을 경우에는 null을 반환하고 해당 노드를 삭제하면 된다
    노드에 자식이 하나 있다면 현재 자식을 반환하고 해당 자식이 위 단계로 올라가서 부모를 대체해야 한다
    노드에 자식이 두개 있다면 왼쪽 하위 트리의 최대치를 찾거나 오른쪽 하위 트리 최소치를 찾아서 해당 노드를 대체한다
  */
  remove (value) {
    return deleteRecursively(this._root, value);

    function deleteRecursively(root, value) {
      if (!root) {
        return null;
      } else if (value < root.value) {
        root.left = deleteRecursively(root.left, value);
      } else if (value > root.value) {
        root.right = deleteRecursively(root.right, value);
      } else {
        if (!root.left && !root.right) { 
          return null;
        } else if (!root.left) {
          root = root.right;
          return root;
        } else if (!root.right) {
          root = root.left;
          return root;
        } else {
          let temp = findMin(root.right);
          root.value = temp.value;
          root.right = deleteRecursively(root.right, temp.value)
          return root;
        }
      } 
      return root;
    }

    function findMin(root) { // 이진트리에서 가장 왼쪽에 있는 값은 최소값이다
      while(root.left) {
        root = root.left;
      }
       return root;
    }
  } // remove() end

  findNode(value) {
    let curRoot = this._root,
        found = false;

    while (curRoot) {
      if (curRoot.value > value) {
        curRoot = curRoot.left
      } else if (curRoot.value < value) {
        curRoot= curRoot.right
      } else {
        found = true;
        break;
      }
    }
    return found;
  }
}

AVL 트리는 스스로 균형을 잡는 이진 검색 트리로, 트리의 높이를 최소로 유지하면서 검색과 삽입, 삭제 연산의 시간 복잡도 O(log2(n))을 보장한다

class AVLTree {
  constructor (value) {
    this.left = null;
    this.right = null;
    this.value = value;
    this.depth = 1;
  }
  
  setDepthBasedOnChildren() {
    if (this.node === null) this.depth = 1;

    if (this.left !== null) this.depth = this.left.depth + 1;

    if (this.right !== null && this.depth <= this.right.depth) {
      this.depth = this.right.depth + 1;
    }
  }
  // 삽입 이후에 균형을 유지하기 위해 자식들을 회전
  rotateRR() {
    let valueBefore = this.value;
    let leftBefore = this.left;
    this.value = this.right.value;

    this.left = this.right;
    this.right - this.right.right;
    this.left.right = this.left.left;
    this.left.left = leftBefore;
    this.left.value = valueBefore;

    this.left.setDepthBasedOnChildren();
    this.setDepthBasedOnChildren();
  }

  rotateLL() {
    let valueBefore = this.value;
    let rightBefore = this.right;
    this.value = this.left.value;

    this.right = this.left;
    this.left - this.left.left;
    this.right.left = this.right.right
    this.right.right = rightBefore;
    this.right.value = valueBefore;

    this.right.setDepthBasedOnChildren();
    this.setDepthBasedOnChildren();
  }

  // 만약 한번 회전을 하고 나서도 AVL 트리가 여전히 불균형이라면 완전한 균형을 위해 두 번 회전해야 함 
  balance() {
    let ldepth = this.left === null ? 0 : this.left.depth;
    let rdepth = this.right === null ? 0 : this.right.depth;
    
    if (ldepth > rdepth + 1) {
      let lldepth = this.left === null ? 0 : this.left.depth;
      let lrdepth = this.right === null ? 0 : this.right.depth;

      if (lldepth < lrdepth) {
        // LR 회전은 왼쪽 자식의 RR회전과 현재 노드의 LL회전으로 구성된다
        this.left.rotateRR();
      }
      this.rotateLL();
    } else if (ldepth + 1 < rdepth) {
      let rrdepth = this.right.right === null ? 0 : this.right.right.depth;
      let rldepth = this.right.left === null ? 0 : this.right.left.depth;

      if (rldepth > rrdepth) {
        // RR회전은 오른쪽 자식의 LL회전과 현재 노드의 RR회전으로 구성됨
        this.right.rotateLL();
      }
      this.rotateRR();
    }
  } // balance() end

  insert (value) {
    let childInserted = false;
    if (value === this.value) {
      return false;
    } else if (value < this.value) {
      if (this.left === null) {
        this.left = new AVLTree(value);
        childInserted = true;
      } else {
        childInserted = this.left.insert(value);
        if (childInserted === true) this.balance();
      }
    } else if (value > this.value) {
      if (this.right === null) {
        this.right = new AVLTree(value);
        childInserted = true;
      } else {
        childInserted = this.right.insert(value);
        if(childInserted === true) this.balance();
      }
    }
    if (childInserted === true) this.setDepthBasedOnChildren();
    return childInserted;
  } // insert() end

  remove(value) {
    return deleteRecursively(this, value);

    function deleteRecursively(root, value) {
      if (!root) {
        return null;
      } else if (value < root.value) {
        root.left = deleteRecursively(root.left, value);
      } else if (value > root.value) {
        root.right = deleteRecursively(root.right, value);
      } else {
        if (!root.left && !root.right) {
          return null;
        } else if (!root.left) {
          root = root.right;
          return root;
        } else if (!root.right) {
          root = root.left;
          return root;
        } else {
          let temp = findMin(root.right);
          root.value = temp.value;
          root.right = deleteRecursively(root.right, temp.value);
          return root;
        }
      }
      root.setDepthBasedOnChildren();
      return root;
    }

    function findMin(root) {
      while (root.left) root = root.left;
      return root;
    }
  } // remove() end
}

이진 검색 트리는 검색에는 매우 뛰어나지만 삽입과 삭제의 연산 시간 복잡도가 O(log2(n))으로 느림
트리가 불균형이 되면 모든 연산이 O(n)이 되니 이를 개선하기 위해 AVL 트리와 같은 자가 균형 트리를 사용해야 한다

주어진 이진트리에서 두 개의 노드의 가장 가까운 공통 조상 찾기

function findLowestCommonAncester(root, value1, value2) {
  function findLowestCommonAncesterHelper(root, value, value2) {
    if (!root) return;
    if (Math.max(value1, value2) < root.value)
      return findLowestCommonAncesterHelper(root.left, value1, value2);
    if (Math.min(value1, value2) > root.value)
      return findLowestCommonAncesterHeleper(root.right, value1, value2);
    return root.value;
  }
  return findLowestCommonAncesterHelper(root, value1, value2);
}

루트의 n번째 거리에 있는 노드 출력하기

const printKthLevels = (root, k) => {
  let arrayKth = [], queue = [];

  if (!root) return;

  queue.push([root, 0]);

  while(queue.length) {
    let tuple = queue.shift(),
        temp = tuple[0];
        height = tuple[1];
    if (height === k) {
      arrayKth.push(temp.value);
    }
    if (temp.left) 
      queue.push([temp.left, height+1]);
    if (temp.right)
      queue.push([temp.right, height+1]);
  }
  console.log(arrayKth);
}

이진 트리가 다른 트리의 하위 트리인지 확인하기

const isSameTree = (root1, root2) => {
  if (root1 === null && root2 === null) return true;
  if (root1 === null || root2 === null) return false;

  return root1.value === root2.value 
    && isSameTree(root1.left, root2.left) 
    && isSameTree(root1.right, root2.right)
}

const checkIfSubTree = (root, subtree) => {
  let queue = [], counter = 0;

  if(!root) return;

  queue.push(root);

  while (queue.length) {
    let temp = queue.shift();
    if (temp.data === subtree.data === isSameTree(temp, subtree)) {
      return true
    }
    if (temp.left)
      queue.push(temp.left);
    if (temp.right)
      queue.push(temp.right);
  }
  return false;
}

트리가 다른 트리와 대칭인지 확인하기

/*
1. 두 트리의 루트 노드 키가 동일해야 함
2. 트리 a의 루트 왼쪽 하위 트리와 트리 b의 오른쪽 하위 트리가 대칭
3. 트리 a의 오른쪽 하위 트리와 트리 b의 왼쪽 하위 트리가 대칭
*/

const isMirrorTrees = (tree1, tree2) => {
  // 기저의 경우 둘 다 빈 상태
  if (!tree1 && !tree2) return true;
  // 둘 중 하나가 빈 상태라면 대칭이 아님
  if (!tree1 || !tree2) return false;

// 한쪽 트리의 왼쪽 하위 트리와 다른 트리의 오른쪽 하위 트리를 전달
  let checkLeftwithRight = isMirrorTrees(tree1.left, tree2.right),
      checkRightwithLeft = isMirrorTrees(tree2.right, tree1.left);
  return tree1.value === tree2.value && checkLeftwithRight && checkRightwithLeft;
}

Comment and share

OLDER POSTS
page 1 of 5

5장 연습문제 다시 보기

스킬트리

괄호 변환

소수 찾기(레벨2)

소수 만들기

신규 아이디 추천

키패드 누르기

하샤드 수

크레인 인형뽑기 게임

다트 게임

폰켓몬

가장 큰 정사각형 찾기

다음 큰 숫자

올바른 괄호

기능개발

가장 큰 수

프린터

19장 동적 프로그래밍

20장 비트 조작

18장 고급 문자열

16장 힙

17장 그래프

15장 트리

Harry Kim