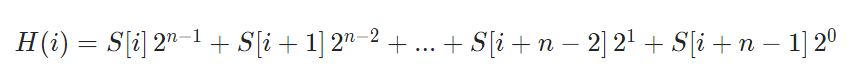21-03-22 알고리즘 문제풀기 및 노트 정리

Mar 22, 2021 in 알고리즘

크레인 인형뽑기 게임

stack 배열을 생성하고 인형을 차례대로 담으면서 이전에 추가한 인형(stack의 마지막값)과 같은지 비교해서 score 계산을 해 주면 된다

function solution(board, moves) {
    let stack = [];
    let score = 0;
    for(let i = 0; i < moves.length; i++) {
        let move = moves[i]-1; // x좌표를 구함 (index는 1부터 시작하므로 1을 빼줌)
        for (let j = 0; j <board.length; j++){ // board 길이만큼 돌고
            if (board[j][move] !== 0) { // 해당 좌표에 있는 인형이 0이 아니고
                if (board[j][move] === stack[stack.length-1] && stack.length > 0){
                    // 이전에 추가한 인형과 값이 같다면 stack에서 빼주고 scoring하기
                    stack.pop();
                    score += 2
                } else {
                    // 값이 다르다면 그냥 stack에 push만 하기
                    stack.push(board[j][move])
                }
                // 해당 인형은 옮겼으니 0으로 바꿔 다시 선택하지 않도록 하기
                board[j][move] = 0;
                break;
            } 
        }
    }
    return score;
}

다트 게임

해당 문제 링크

처음에 혼자 풀 때 짰던 코드
스타상이 이전 점수에도 영향을 준다는 것을 고려하지 못함

또, 10점을 고려하기 위해 같은 코드가 반복되어 지저분해보임

function solution(dartResult) {
    let answer = 0;
    let split = dartResult.split('');
    let dartScore = 0, alphabet = '', powValue = 0, starOrSharp = '';
    while (split.length > 0){
        if (split[1] === '0') {
            dartScore = split.shift() * 10;
            split.shift();
            alphabet = split.shift();
            powValue = alphabet === 'S' ? 1 : alphabet === 'D' ? 2 : 3
            if (split[0] === '*' || split[0] === '#') {
                starOrSharp = split.shift() === '*' ? 2 : -1;
            } else {
                starOrSharp = 1;
            }
            answer += Math.pow(dartScore, powValue) * starOrSharp;
        } else if (split[1] !== '0') {
            dartScore = split.shift() * 1;
            alphabet = split.shift();
            powValue = alphabet === 'S' ? 1 : alphabet === 'D' ? 2 : 3
            if (split[0] === '*' || split[0] === '#') {
                starOrSharp = split.shift() === '*' ? 2 : -1;
            } else {
                starOrSharp = 1;
            }
            answer += Math.pow(dartScore, powValue) * starOrSharp;
        }
    }
    return answer;        
}

다른분 풀이
Object로 S, D, T값을 설정해 찾아 쓰는 방식은 O(1)로 가능하므로 보고 배워야겠다는 생각을 함

스택 구조를 만들고 스택 내에 점수를 하나씩 저장해놓고 스타상이 두번째에 온다면 스택 내 값을 수정하는 방식을 미처 생각치 못함


function solution(dartResult) {
    let stack = [];
    let score = {
        S: 1,
        D: 2,
        T: 3
    }
    let count = 0;
    const len = dartResult.length;
    
    for (let i = 0; i < len; i++) {
        let isChar = dartResult.charAt(i);
        if (+isChar != isChar) {
            if(score[isChar]) {
                stack.push(Math.pow(dartResult.slice(i - count, i), score[isChar]));
                count = 0;
            } else {
                const sharpOrStar = isChar === '*' ? 2 : -1;
                const stackLen = stack.length;
                if (sharpOrStar == 2 && stackLen > 1) {
                    stack[stackLen-2] = stack[stackLen-2] * sharpOrStar;
                }
                stack[stackLen-1] = stack[stackLen-1] * sharpOrStar;
            }
        } else {
            count++;
        }
    }
    return stack.reduce((acc, cur) => acc+ cur, 0)
}

폰켓몬

해당 문제 링크

처음에 든 생각은 그냥 set에 넣고 unique한 값만 뽑으면 되는 것 아닌가? 했음
문제에서 폰켓몬은 N/2마리를 선택해야 하므로 만약에 들어오는 배열의 길이를 반으로 나눈 값이 set의 사이즈보다 작다면 단순히 배열 길이를 반으로 나눈 값을 리턴하면 될 일이었음

function solution(nums) {
    let answer = 0;
    let set = new Set ();
    for(let number of nums){
        set.add(number);
    }

    if(set.size < nums.length/2) {
        answer = set.size;
    } else { 
        answer = nums.length/2;
    }
    return answer;
}

Comment and share

21-03-21 알고리즘 문제풀기 및 노트 정리

Mar 21, 2021 in 알고리즘

가장 큰 정사각형 찾기

해당 문제 링크

1과 0으로 채워진 표가 있고 1로 이루어진 정사각형 중 가장 큰 정사각형의 넓이를 리턴하는 문제

DP를 사용해 풀어야 한다

function solution (board) {
    let lengthY = board.length;
    let lengthX = board[0].length;
    let max = 0;
    if(lengthX < 2 || lengthY <2) {
        return 1;
    }

    for(let i = 1; i < lengthY; i++) {
        for(var j=1; j< lengthX; j++) {
            if(board[i][j] > 0) {
                board[i][j] = Math.min(
                    board[i-1][j-1], // 좌상단
                    board[i][j-1],   // 왼쪽
                    board[i-1][j])   // 오른쪽
                    + 1              // 현재값
            } 

            if(max < board[i][j]){
                max = board[i][j]
            }
        }
    }
    return Math.pow(max, 2)
}

다음 큰 숫자

해당 문제 링크

1
2
3

조건 1. n의 다음 큰 숫자는 n보다 큰 자연수 입니다.
조건 2. n의 다음 큰 숫자와 n은 2진수로 변환했을 때 1의 갯수가 같습니다.
조건 3. n의 다음 큰 숫자는 조건 1, 2를 만족하는 수 중 가장 작은 수 입니다.

내 풀이

function solution (n) {
    let largeNumber = n; // 나중에 리턴할 값
    let binary = n.toString(2).split(''); // n을 2진수로 바꾸고
    let cntOne = binary.filter(num => parseInt(num,10) > 0).length; // 1의 갯수를 filter하여 카운트
    
    while(true) {
        largeNumber++; // 값을 증가시키고
        let lnBinary = largeNumber.toString(2).split('') // 같은 방법으로 2진수로 변환하고
        let cntThisOne = lnBinary.filter(num => parseInt(num, 10) > 0).length; // 1의 갯수를 같은 방법으로 카운트
        if (cntThisOne === cntOne) // 만약에 n의 이진수가 갖는 1의 개수가 원래 값의 1의 개수랑 같다면 빠져나가기
            break;
    }
    return largeNumber;
}

시프트 연산자를 사용한 해법

function nextBigNumber(n) {
    var i, j;
    for (i = 0; !(n & 1); i++) {
        n = n >> 1; 
        } // 1을 찾을때까지 우로 쉬프트, 쉬프트 횟수 = i
    for (j = 0; n & 1; i++, j++) {
        n = n >> 1; 
        } // 0을 찾을때까지 우로 쉬프트, 1의 갯수 = j
    for (j--, n++; i !== j; i--) {
        n = n << 1; 
        } // 0자리에 1대입, 1의 갯수 -1, i === j 가 될때까지 죄로 쉬프트하면서 쉬프트 횟수 -1
    for (i; i; i--, n++) {
        n = n << 1; 
        } // i === 0 될때까지 좌로 쉬프트 하면서 쉬프트 횟수 -1, 0자리에 1대입
    return n;
}

올바른 괄호

해당 문제 링크

function solution(s){
    let stack = [];
    let split = s.split('')

    if (split[0] === ')') return false;

    console.log(split);
    console.log(stack);

    while(split.length > 0) {
        // 만약에 split[0]이 '(' 괄호라면 split에서 빼서 stack에 넣음
        if (split[0] === '(')
            stack.push(split.shift()); 
        // 만약에 split[0]이 ')'이고
        else {
            // stack에 '('가 있다면
            if (stack.includes('(')){
                stack.pop(); // 마지막으로 넣은 괄호를 빼고
                split.shift(); // split내에서도 하나 빼기
                console.log("stack", stack)
                console.log("split", split)
            } else {
                return false;
            }
        }
    }
    
    return stack.length > 0 ? false : true;
}

이 풀이는 효율성 테스트를 통과하지 못함
while문을 사용한 것이 문제였을까?

필터를 사용해보기로 했다

let split = s.split('')
   if (split[0] === ')') return false;
   let countLeft = split.filter(branket => branket === '(').length;
   let countRight = split.filter(branket => branket === ')').length;

   return countLeft === countRight ? true : false;

테스트 케이스를 통과하지 않는 경우가 있어 실패…

else if 케이스를 만들어서 가능한 수를 하나 더 고려해야 했음

function solution2_1(s) {
    let answer = true; 
    let left = 0; 
    let split = s.split('');

    for(let item of split) {
        if (item === '(') { // 왼쪽 괄호를 찾으면 left를 더해준다
            left++
        } else if (left > 0) { // 만약 '('가 아니라면 ')'일 것이고 그렇다면 left를 줄여준다
            left--
        } else { // 이 둘 다 아니라면 괄호의 짝이 없다는 뜻
            return false;
        }
    }

    answer = left === 0 ? true : false; // left가 0이 아니라면 false 일 것
    return answer;
}

Comment and share

21-03-17 알고리즘 문제풀기 및 노트 정리

Mar 17, 2021 in 알고리즘

기능개발

해당 문제 링크

앞에 있는 기능이 배포될 때 함께 배포된다 는 뜻이 선입선출식 자료구조를 사용하라는 뜻이었음

progresses와 speeds는 짝을 이루는 구조(같은 index값을 갖는 구조)

1. 한 번의 루프마다 progresses[index] + speeds[index]를 한다
    1-1. 만약 이때 값이 100을 넘었다면 해당 원소들을 각각 shift()한다
    1-2. cnt++과 더불어 index값을 줄여준다(원소를 뺐으므로)
    1-3. cnt값이 0이 아니라면 정답 배열에 넣어준다
2. 정답 배열을 리턴한다

function solution(progresses, speeds) {
    let answer = [];
    let cnt = 0; // 한번에 배포되는 기능 수

    while(progresses.length > 0) {
        progresses = progresses.map((el, index) => el + speeds[index]); 
        for (let i = 0, len = progresses.length; i < len; i++) {
            if(progresses[i] >= 100) {
                progresses.shift();
                speeds.shift();
                cnt++;
                i--;
            } else break;
        }

        if (cnt > 0) {
            answer.push(cnt); // 한번에 배포될 기능 수를 넣어줌
            cnt = 0; // 0으로 초기화
        }
    }
    return answer;
}

다른 방법

1 2	1. 각 기능마다 걸리는 시간을 소수점자리 올림으로 계산하여 배열을 만듦 2. 이 배열의 가장 처음값을 빼 변수로 저장하고 이 값을 기준으로 나머지

function solution(progresses, speeds) {
    let answer = [];
    let daysLeft = progresses.reduce((acc, cur, index) => {
        let day = Math.ceil((100-cur)/speeds[index]);
        acc.push(day);
        return acc;
    }, [])

    let func = daysLeft[0]
    let cnt = 1;
    for (let i = 1; i < daysLeft.length; i++) {
        if (func >= daysLeft[i]) 
            cnt++;
        else {
            answer.push(cnt);
            cnt = 1;
            func = daysLeft[i];
        }
        if (i === daysLeft.length-1)
            answer.push(cnt);
    }
    return answer;
}

이 방법은 작업 완료에 걸리는 일 수를 기준으로 배열을 돌며 배포할 기능 수를 push하는 방법

가장 큰 수

해당 문제 링크

처음에는 탐욕법으로 풀어야 하나 했는데 sort함수 하나로 해결 가능한 문제였음

테스트 케이스 11번이 0으로만 된 배열이 들어오므로 정수화(parseInt)해서 0이라면 “0”을 리턴하도록 해야 했음

function solution(numbers) {
    let answer = numbers.map(num => '' + num)
                            .sort((a,b) => (b+a) - (a+b))
                            .join('')
    return parseInt(answer,10) === 0 ? "0" : answer;
}

프린터

해당 문제 링크

1
2
3

1. 인쇄 대기목록의 가장 앞에 있는 문서(J)를 대기목록에서 꺼냅니다.
2. 나머지 인쇄 대기목록에서 J보다 중요도가 높은 문서가 한 개라도 존재하면 J를 대기목록의 가장 마지막에 넣습니다.
3. 그렇지 않으면 J를 인쇄합니다.

function solution(priorities, location) {
    let answer = 0;
    let queue = [...priorities]; // 프린트 큐에 깊은 복사
    let myPrint = location; 
    
    while (queue.length){ 
        // 프린트 큐 맨 처음 있는 작업보다 우선도가 더 크다면
        if (queue.some(priority => priority > queue[0])){
            // 첫 작업을 shift한 후 맨 마지막으로 push한다
            queue.push(queue.shift());
            if (myPrint === 0){
                myPrint += queue.length - 1;
            } else {
                // 인덱스 값은 0에서부터 시작되므로 -1 해주어야 함
                myPrint -= 1;
            }
        } else { 
        // 프린트 큐 맨 처음 작업이 제일 우선도가 높다면
            queue.shift(); // 해당 작업을 shift하고
            answer += 1; // 해답이 해당 작업임
            if (myPrint === 0){
                break;
            } else {
                myPrint -= 1;
            }
        }
    }
    return answer;
}

Comment and share

21-03-16 자바스크립트로 하는 자료구조와 알고리즘(11)

Mar 16, 2021 in 알고리즘, 서적

19장 동적 프로그래밍

동적 프로그래밍(이하 DP)은 문제를 더 작은 부분들로 쪼개는 과정이 포함된다
해시 테이블을 사용한다면 이미 계산된 피보나치 숫자를 저장할 수 있고 계산 없이 O(1)의 시간으로 그 값을 불러올 수 있기 때문에 더 빠르게 구현할 수 있다
1
2
3
4
5
6
let cache = {};
const fiboBest = n => {
if (n <= 1) return n;
if(cache[n]) return cache[n];
return (cache[n] = fiboBest(n-1) + fiboBest(n-2));
}
DP는 재계산을 피하기 위해 이미 계산된 값들을 저장하고 해당 값들을 사용하는 방법이다
- 중복 부분 문제 : DP에서 보통 문제의 해결책으로 해시 테이블과 배열, 행렬에 저장하는 방식을 사용하는데, 이 방식을 메모이제이션이라고 부른다
- 최적 부분 구조 : 문제의 부분 최적 해결책을 통해 큰 문제를 해결하는 방법
배낭 문제 알고리즘은 대표적인 DP의 예로 무게와 가치를 지니는 n개의 항목이 주어졌을 때 최대 w의 무게를 담을 수 있는 배낭에 가치의 최대값을 담는 문제
배열(배낭)에 담긴 n개의 항목이 최대값이 되려면
1. n번째 항목이 제외되는 경우: n-1개의 항목에서 얻은 최대값
2. n번째 항목을 포함하는 경우: n-1개의 항목에서 얻은 최대값 + n번째 항목의 값

동적 프로그래밍의 구현은 현재 배열 인덱스와 목표치를 객체에 대한 키로 사용해 결과를 저장함 (메모이제이션 활용)

const knapsackDP = (idx, weights, values, target, matrix) => {
  let result = 0;
  if(matrix[idx + '-' + target]) {
    return matrix[idx + '-' + target]
  }

  if(idx <= -1 || target <= 0) {
    result = 0
  } else if (weights[idx] > target) {
    result = knapsackDP(idx - 1, weights, values, target, matrix);
  } else {
    let current = knapsackDP(idx - 1, weights, values, target, matrix),
        currentPlusOther = values[idx] + knapsackDP(idx - 1, weights, values, target - weights[idx], matrix);
    result= Math.max(current, currentPlusOther);
  }
  matrix[idx + '-' + target] = result
  return result;
}

최장 공통 부분 수열 알고리즘
두 개의 수열이 있을 때 두 수열의 가장 긴 공통 부분 수열의 길이를 찾는 알고리즘
부분 수열 내 항목들이 연속일 필요는 없고 순서만 맞으면 됨

길이 m인 문자열 str1과 길이 n인 문자열 str2가 함수 LCS를 통해 최장 공통 부분을 구한다면

if (두 수열의 마지막 글자가 일치한다면) {
  result = 1 + LCS(X[0:m-2], Y[0:n-2])
}
if (두 수열의 마지막 글자가 일치하지 않는다면) {
  result = Math.max(LCS(X[0:m-1], Y[0:n-1]), LCS(X[0:m-2], Y[0:n-2]))
}

재귀를 기반으로 의사 코드를 구현

const LCSNaive = (str1, str2, str1Length, str2Length) => {
  if (str1Length === 0 || str2Length === 0) {
    return 0;
  }

  if (str1[str1Length-1] === str2[str2Length-1]) {
    return 1 + LCSNavie(str1, str2, str1Length - 1, str2Length - 1);
  } else {
    return Math.max(
      LCSNavie(str1, str2, str1Length, str2Length - 1),
      LCSNavie(str1, str2, str1Length - 1, str2Length)
      )
  }
}

const LCSNaiveWrapper = (str1, str2) => {
  return LCSNaive(str1, str2, str1.length, str2.length);
}

DP식 접근법

const longestCommonSequenceLength = (str1, str2) => {
  let matrix = Array(str.length + 1).fill(Array(str2.length + 1).fill(0)), 
      rowLength = str1.length + 1,
      colLength = str2.length + 1,
      max = 0;
  for (let row = 1; row < rowLength; row++) {
    for (let col = 1; col < colLength; col++) {
      let str1Char = str1.charAt(row - 1),
          str2Char = str2.charAt(col - 1);
      
      if (str1Char === str2Char) {
        matrix[row][col] = matrix[row - 1][col - 1] + 1;
        max = Math.max(matrix[row][col], max);
      }
    }
  }
  return max;
}

동전 교환 알고리즘 : 동전의 금액 종류 M개가 들어있는 객체 S가 주어질때 금액 n을 동전으로 교환하기 위한 조합을 구하는 문제

이때 이 문제의 최적 부분 구조는 (1) M번째 동전이 포함되지 않는 해결책과 (2) M번째 동전이 최소 한 개 포함되는 해결책 으로 나눌 수 있다
coinChange(S, M, n) = coinChange(S, M-1, N) + coinChanges(S, M, N-Sm)

// coinArr의 인덱스는 [0, ..., coinIndex]
const countCoinWays = (coinArr, coinIndex, total) => {
  if (total === 0) return 1;
  // total 값이 0에 도달한 경우에는 아무 동전도 포함하지 않는 것
  if (total < 0 || (coinIndex <= 0 && total >= 1)) return 0;
  // total값이 0 보다 작다는 것은 M번째 동전이 포함되거나 포함되지 않을 때의 해결책이 없다는 뜻
  // 남은 동전이 없을 때 (index값은 coinArr.length에서 점점 줄어드므로) total값을 채우지 못해도 해결책이 없다는 뜻

  return countCoinWays(coinArr, coinIndex - 1, total) +
        countCoinWays(coinArr, coinIndex - 1, total - coinArr[coinIndex - 1])
}
const countCoinWaysWrapper = (coinArr, total) => {
  return countCoinWays(coinArr, coinArr.length, total);
}

하지만 이 방법을 사용한다면 중복 부분 문제가 많다

동전 교환 알고리즘을 DP로 구현하기

const countCoinWaysDP = (coinArr, coinIndex, total) => {
  let dpMatrix = [];
  // 메모이제이션용 행렬, 추후 2차원 배열이 된다
  for (let i = 0; i <= total; i++) {
    dpMatrix[i] = [];
    // 원하는 값까지 전부 배열이 들어가게 된다
    for (let j = 0; j < coinIndex; j++) {
      dpMatrix[i][j] = undefined;
      // undefined로 초기화
    }
  }

  for (let i = 0; i < coinIndex; i++) {
    // 맨 윗줄을 1로 채움 (undefined에서 기본값으로)
    dpMatrix[0][i] = 1;
  }

  for (let i = 1; i < total + 1; i++) {
    // 행렬의 세로이동
    for (let j = 0; j < coinIndex; j++) {
      // 행렬의 가로이동
      let temp1 = 0, temp2 = 0;
      // 두 가지의 부분 방법으로 나뉘므로 temp값도 두개가 필요함
      if (i - coinArr[j] >= 0) {
        temp1 = dpMatrix[i - coinArr[j]][j];
        // temp1값에 dpMatrix[0][0] 번값부터 가로줄 값을 저장
      }

      if (j >= 1) {
        temp2 = dpMatrix[i][j-1];
        // temp2값에 dpMatrix[1][0] 값부터  세로줄 값을 저장
      }
      
      // dpMatrix[1][0] 값부터 temp1(M번째 동전이 포함되지 않는 해결책)값과 
      // temp2(M번째 동전이 최소한 한 개 포함되는 해결책)값을 더해 저장
      dpMatrix[i][j] = temp1 + temp2;
    }
  }

  // 결과값이 저장되어있는 것 중에서 total값을 만족하는 행의 max값을 리턴함 
  // if()에서도 i < coinIndex 와 같이 리턴하였으므로 여기서도 -1 해주어야 함
  return dpMatrix[total][coinIndex - 1]
}

const countCoinWaysDPWrapper = (coinArr, coinValue) => {
  return countCoinWaysDP(coinArr, coinArr.length, coinValue);
}

편집 거리 알고리즘 (레벤슈타인 거리 알고리즘)

길이 m인 문자열 str1과 길이 n인 문자열 str2가 주어졌을때 str1을 str2로 변환하기 위환 최소 편집 횟수는? (이 때, 사용가능한 연산은 삽입, 제거, 교환만 가능하다)

if (문자가 동일하다)
  아무것도하지 않는다
if (문자가 다르다) {
  1) m과 n-1의 삽입
  2) m-1과 n의 제거
  3) m-1과 n-1의 교환 
  세가지를 재귀적으로 고려
}

Brute-force 방법으로 구현하기

const editDistanceRecursive = (str1, str2, length1, length2) => {
  // 빈문자열이라면 나머지 한 쪽의 문자열을 그대로 복사하면 되므로 나머지 한 쪽 길이값을 리턴함 (length1 or length2번 시행해야 하므로)
  if (length1 === 0) return length2;
  if (length2 === 0) return length1;

  // 마지막 글자가 같다면 마지막 글자를 제외한 나머지 문자만큼 돌면 된다
  // 이 과정은 재귀적으로 반복되므로 맨 마지막 글자부터 첫번째 글자까지 비교를 할 것
  if (str[length1-1] === str2[length2-1]) 
    return editDistanceRecursive(str1, str2, length1-1, length2-1)

  return 1 + Math.min(
    editDistanceRecursive(str1, str2, length1, length2-1), // 삽입
    editDistanceRecursive(str1, str2, length1-1, length2), // 제거
    editDistanceRecursive(str1, str2, length1-1, length2-1) // 교환
  )
}

const editDistanceRecursiveWrapper = (str1, str2) => {
  return editDistanceRecursive(str1, str2, str1.length, str2.length)
}

DP식 접근법

const editDistanceDP = (str1, str2, length1 = str1.length, length2 = str2.length2) => {
  let dpMatrix = [];
  for (let i = 0; i < length1+1; i++) {
    dpMatrix[i] = [];
    for (let j = 0; j < length2+1; j++) {
      dpMatrix[i][j] = undefined;
    }
  }
  // let dpMatrix = Array.from({length: length1+1}, 
  //           () => Array.from({length:length2+1}, () => undefined))

  for (let i = 0; i < length+1; i++) {
    for (let j = 0; j < length2+1; j++) {
      if (i === 0) {
        dpMatrix[i][j] = j;
      } else if (j === 0) {
        dpMatrix[i][j] = i;
      } else if (str1[i-1] === str2[j-1]) {
        dpMatrix[i][j] = dpMatrix[i-1][j-1];
      } else {
        let insertCost = dpMatrix[i][j-1],
            removeCost = dpMatrix[i-1][j],
            replaceCost = dpMatrix[i-1][j-1];

        dpMatrix[i][j] = 1 + Math.min(insertCost, removeCost, replaceCost)
      }
    }
  }
  return dpMatrix[length1][length2];
}

20장 비트 조작

고성능 서버 사이드 코드를 구현하길 원한다면 비트 조작도 알아야 함
자바스크립트의 비트 연산자
&는 AND, |는 OR, ~는 NOT, ^는 XOR에 해당하고 왼쪽 이동은 <<로, 오른쪽 이동은 >>로, >>>는 오른쪽 이동 후에 0으로 채운다는 뜻이다
AND 연산자(&)는 두 개의 비트가 모두 1일때 참이다
a = 1100, b = 1010일 때, a & b = 1000이다
OR 연산자(|)는 두 개의 비트 중 하나만 1이어도 참이다
a = 1100, b = 1010일 때, a & b = 1110이다
XOR 연산자(^)는 비트 중 하나가 1일 때만 참이 된다
a = 1100, b = 1010일 때, a & b = 0110이다
NOT 연산자는 모든 비트를 뒤집는다
a = 1100일 때 NOT a = 0011이다
왼쪽 이동 연산자(<<)는 모든 비트가 왼쪽으로 이동되고 왼쪽 끝 범위를 벗어나는 비트는 버려진다
9(1001) << 1 = 10010(2) = 18, 9 << 2 = 100100(2) = 36
위 예와 같이 왼쪽 이동 연산자는 해당 항목을 두 배로 증가시킨다 (이진 연산 체계이기 때문) 하지만 왼쪽 이동으로 비트가 넘친다면 버려지므로 값이 작아질 수 있다
오른쪽 이동 연산자(>>)는 모든 비트가 오른쪽으로 이동되고 오른쪽 끝 범위를 벗어나면 버려진다
9(1001) >> 1 = 100(2) = 4
오른쪽 이동 연산자는 항목을 2로 나눈 값이 된다

비트 연산자를 사용해 연산해보기

// 이진수를 더하기는  두 수를 더한 다음 10을 초과하면 1을 다음 수로 올린다 (carry)
const BitwiseAdd = (a, b) => {
  while (b !== 0) {
    let carry = (a & b);
    a = a ^ b;
    b = carray << 1;
  }
  return a;
}

// 이진수에서 음의 이진수로부터 양의 이진수를 빼려면 모든 비트를 뒤집은 다음 1을 더하면 된다
const BitwiseNegate = a => {
  return BitwiseAdd(~a, 1);
}

// 빼기는 음수를 더하는 것이기 때문에 음의 이진수를 구하고 더한다
const BitwiseSubtract = (a, b) => {
  return BitwiseAdd(a, BitwiseNegate(b))
}

// 곱셈은 두 수를 곱하고 10이 넘어가는 수는 다음 자릿수로 올리고 다음 자릿수로 이동해 해당 자릿수의 수를 곱한다
const BitwiseMultiply = (a, b) => {
  let m = 1, c = 0;
  if (a < 0) {
    a = BitwiseNegate(a);
    b = BitwiseNegate(b);
  }

  while (a >= m && b) {
    if (a & m) 
      c = BitwiseAdd(b, c);
    b = b << 1;
    m = m << 1;
  }
  return c;
}

// a나누기 b는 b를 여러번 빼는 것이라고 생각하면 쉽다
const BitwiseDividePositive = (a, b) => {
  let c = 0;
  if (b !== 0) {
    while (a >= b) {
      a = BitwiseSubtract(a, b);
      c++
    }
  }
  return c;
}

// 하지만 음의 정수를 나누기한다면 while값이 무한히 반복될 것이기 때문에 부호를 저장할 값이 필요하다
const BitwiseDivide = (a, b) => {
  let c = 0, isNegative = 0;

  if (a < 0) {
    a = BitwiseNegate(a);
    isNegative = !isNegative;
  }

  if (b < 0) {
    b = BitwiseNegate(b);
    isNegative = !isNegative;
  }

  if (b !== 0) {
    while (a >= b) {
      a = bitwiseSubstract(a, b);
      c++;
    }
  }

  if (isNegative) {
    c = BitwiseNegate(c);
  }
  return c;
}

비트연산자는 Math의 기본 함수보다 빠르다
최근의 자바스크립트는 Node.js를 활용해 서버 측 프로그래밍에 진입하고 있기 때문에 비트 연산자는 효율적인 코드를 만드는데 도움이 될 것이다

Comment and share

21-03-15 자바스크립트로 하는 자료구조와 알고리즘(10)

Mar 15, 2021 in 알고리즘, 서적

18장 고급 문자열

트라이(trie)는 문자열을 검색해 저장된 문자열 중 일치하는 문자열이 있는지 확인하는데 주로 사용되는 특별한 종류의 트리

트라이는 중첩 객체를 사용해 구현되는데 각 노드는 자신과 직접 연결된 자식들을 지니고 이 자식들은 키 역할을 한다

class TrieNode {
  constructor() {
    this.children = {};
    this.endOfWord = false;
  }
}

class Trie {
  constructor() {
    this.root = new TrieNode(); // 생성되면 하나의 트라이 노드를 갖는다
  }

  insert(word) {
    let current = this.root; // 현재 노드값을 가져옴 이 노드에는 children 객체와 endOfWord가 존재함
    for (let i = 0, len = word.length; i < len; i++){
      let ch = word.charAt(i);
      let node = current.children[ch]; // 객체(children{})내 항목 참조
      if (node === null) {
        node = new TrieNode();
        current.children[ch] = node;
      }
      current = node;
    }
    current.endOfWord = true;
  }

  search(word) {
    let current = this.root;
    for (let i = 0, len = word.length; i < len; i++) {
      let ch = word.charAt(i);
      let node = current.children[ch]; 
      if (node === null) {
        return false;
      }
      current = node;
    }
    return current.endOfWord;
  }

  delete(word) {
    this.deleteRecursively(this.root, word, 0);
  }

  deleteRecursively(current, word, index) {
    if (index === word.length) {
      if (!current.endOfWord) return false
      current.endOfWord = false;
      return Object.keys(current.children).length === 0;
    }
    let ch = word.charAt(index),
        node = current.children[ch];
    
    if (node === null) return false;
    let shouldDeleteCurrentNode = this.deleteRecursively(node, word, index+1); 
    // shouldDeleteCurrentNode의 리턴은 boolean값이므로 이 값이 true라면 삭제해야 한다

    if(shouldDeleteCurrentNode) {
      delete current.children[ch];
      return Object.keys(current.children).length === 0;
    }
    return false
  }
}

보이어-무어 문자열 검색

텍스트 편집기 어플리케이션과 웹 브라우저의 ‘찾기’기능에 사용됨

const buildBadMatchTable = str => {
  let tableObj = {},
      strLength = str.length;
  for (let i = 0; i < strLength - 1; i++) {
    tableObj[str[i]] = strLength - 1 - i;
  }
  if (tableObj[str[strLength-1]] === undefined) {
    tableObj[str[strLength-1]] = strLength;
  }
  return tableObj;
}

보이어-무어 문자열 검색 알고리즘의 구현
패턴으로 사용할 문자열을 입력받을 때 검색하고자 하는 현재 문자열이 불일치 표에 존재하면 인덱스를 건너 뛴다

현재 문자열이 불일치 표에 존재하지 않다면 인덱스를 1 증가시킴

const boyerMoore = (str, pattern) => {
  let badMatchTable = buildBadMatchTable(pattern),
      offset = 0,
      patternLastIndex = pattern.length - 1,
      scanIndex = patternLastIndex,
      maxOffset = str.length - pattern.length;
  while (offset <= maxOffset) {
    scanIndex = 0;
    while (pattern[scanIndex] === str[scanIndex + offset]) {
      if (scanIndex === patternLastIndex) {
        return offset;
      }
      scanIndex++;
    }
    let badMatchString = str[offset + patternLastIndex];
    if (badMatchTable[badMatchString]) {
      offset += badMatchTable[badMatchString]
    } else {
      offset += 1;
    }
  }
  return -1;
}

보이어-무어 알고리즘은 최선의 경우 모든 문자가 동일할 때이고 이 때의 시간 복잡도는 O(W/T)이다 (이때, W는 패턴을 찾고자 하는 대상인 문자열)
최악의 경우 패턴이 문자열의 끝에 존재하고 앞부분이 모두 고유의 문자로 구성된 경우고 이 때의 시간 복잡도는 O(T*W)가 된다
이보다 조금 더 빠른 구현을 위해서는 커누스-모리스-플랫 문자열 검색 알고리즘(이후 KMP 알고리즘)을 사용할 수 있다
KMP 알고리즘은 입력 텍스트 T 내에서 단어 W의 출현 횟수를 검색한다
접두사 배열을 만들 때 접두사 배열이 동일한 접두사를 얻기 위해 인덱스를 얼마나 되돌려야 할지를 나타낼 수 있도록 해야 한다

접두사 표 만들고 KMP 검색

const longestPrefix = str => {
  let prefix = new Array(str.length);
  let maxPrefix = 0;
  prefix[0] = 0;
  for (let i = 1, len = str.length; i < len; i++) {
    while (str.charAt(i) !== str.charAt(maxPrefix) && maxPrefix > 0) {
      maxPrefix = prefix[maxPrefix - 1];
    }
    if (str.charAt(maxPrefix) === str.charAt(i)) {
      maxPrefix++;
    }
    prefix[i] = maxPrefix;
  }
  return prefix;
}

const KMP = (str, pattern) => {
  let prefixTable = longestPrefix(pattern),
      patternIndex = 0,
      strIndex = 0;
  while (strIndex < str.length) {
    if (str.charAt(strIndex) !== pattern.charAt(patternIndex)) {
      if (patternIndex !== 0) {
        patternIndex = prefixTable[patternIndex - 1];
      } else {
        strIndex++;
      }
    } else if (str.charAt(strIndex) === pattern.charAt(patternIndex)) {
      strIndex++;
      patternIndex++;
    }

    if (patternIndex === pattern.length) {
      return true;
    }
  }
  return false;
} // 시간 복잡도는 O(W)

라빈-카프 검색 알고리즘은 텍스트에서 특정 패턴을 찾기 위해 해싱을 활용한다
해시 함수(라빈 지문 해싱 기법)를 통해 부분 문자열이 패턴과 동일한지 비교하는 과정의 속도를 높인다
라빈 지문

라빈 지문을 이용한 해시 함수

class RabinKarpSearch {
  constructor () {
    this.prime = 101;
  }

  rabinkarpFingerprintHash (str, endLength) {
    if (endLength === null) endLength = str.length;
    let hashInt = 0;
    for (let i = 0; i < endLength; i++) {
      hashInt += str.charCodeAt(i) * Math.pow(this.prime, i);
    }
    return hashInt;
  }

  recalculate (str, oldIndex, newIndex, oldHash, patternLength) {
    if (patternLength === null) patternLength = str.length;
    let newHash = oldHash - str.charCodeAt(oldIndex);
    newHash = Math.floor(newHash/this.prime);
    newHash += str.charCodeAt(newIndex) * Math.pow(this.prime, patternLength - 1);
    return newHash;
  }

  strEquals (str1, startIndex1, endIndex1, str2, startIndex2, endIndex2) {
    if(endIndex1 - startIndex1 !== endIndex2 - startIndex2) return false;
    while (startIndex1 <= endIndex1 && startIndex2 <= endIndex2) {
      if (str1[startIndex] !== start2[startIndex2]) {
        return false;
      }
      startIndex1++;
      startIndex2++;
    }
    return true;
  }

  rabinkarpSearch (str, pattern) {
    let T = str.length,
        W = pattern.length,
        patternHash = this.rabinkarpFingerprintHash(pattern, W),
        textHash = this.rabinkarpFingerprintHash(str, W);

    for (let i = 1; i <= T - W + 1; i++) {
                                        // strEquals (str1, startIndex1, endIndex1, str2, startIndex2, endIndex2) 
      if (patternHash === textHash && this.strEquals(str, i - 1, i + W - 2, pattern, 0, W - 1)) {
        return i - 1;
      }
      if (i < T - W + 1) {
                    // recalculate (str, oldIndex, newIndex, oldHash, patternLength)
        textHash = this.recalculateHash(str, i - 1, i + W - 1, textHash, null);
      }
    }
    return -1;
  }
}

라빈-카프 알고리즘은 원본 자료가 있는 경우 표절 검사 등에 사용될 수 있다

Comment and share

21-03-14 자바스크립트로 하는 자료구조와 알고리즘(9)

Mar 14, 2021 in 알고리즘, 서적

16장 힙

힙은 O(1) 시간으로 가장 높은 항목이나 가장 낮은 항목을 반환하는 중요한 자료 구조
힙은 트리와 비슷한 자료 구조의 일종으로 최대 힙의 경우 부모가 자식보다 크고 최소 힙의 경우 부모가 자식보다 작다
힙은 자식에 대한 포인터를 갖는 대신에 배열을 사용해 자료를 저장함
배열을 사용하므로 인덱스를 통해 힙 노드의 자식 위치를 쉽게 계산할 수 있다
힙이 배열을 사용해 자료를 저장하기 때문에 인덱스는 각 항목의 차수/높이를 정의 한다
첫 번째 배열 항목을 루트로 설정하고 각 왼쪽 항목과 오른쪽 항목을 순서대로 채워 이진 힙을 만들 수 있다

최대 힙은 루트노드가 가장 높은 값을 갖고 최소 힙은 루트노드가 가장 낮은 값을 갖는다

class Heap {
    // 힙은 배열을 사용해 자료를 저장
    constructor () {
        this.items = [];
    }

    // 두 개의 인덱스에 위치한 값을 바꾸는 것도 인덱스 값으로 변경 가능함
    swap(idx1, idx2) {
        let temp = this.itmes[idx1];
        this.itmes[idx1] = this.items[idx2];
        this.items[idx2] = temp;
    } 

    parentIndex(idx) {
        return Math.floor((idx-1)/2);
    }

    leftChildIndex(idx) {
        return index * 2 + 1;
    }

    rightChildIndex(idx) {
        return idx * 2 + 2;
    }

    parent(idx) {
        return this.items[this.parentIndex(idx)];
    }

    leftChild(idx) {
        return this.items[this.leftChildIndex(idx)];
    }

    rightChild(idx) {
        return this.items[this.rightChildIndex(idx)];
    }

    peek(item) {
        return this.items[0];
    }

    size() {
        return this.items.length;
    }
}

예를들어 최소 힙 구조인 배열이 [2, 4, 23, 12, 13] 라면 부모 노드인 0번 인덱스 2가 부모가 될 것이고 1번 인덱스인 4는 왼쪽 자식이, 2번 인덱스인 23은 오른쪽 자식이 된다
항상 좌측이 먼저 채워지고 우측이 채워지므로 3번 인덱스는 1번 인덱스의 왼쪽 자식이 되고 4번 인덱스는 1번 인덱스의 오른쪽 자식이 된다
정리하면 자신의 인덱스가 N이라고 한다면 부모는 (N - 1)/2 의 인덱스를 가질 것이고(예를 들어 N = 3 일 때, 부모의 인덱스는 1), 왼쪽 자식은 (N * 2) + 1 의 인덱스를, 힙 배열이 순차적이라면 오른쪽 자식은 바로 옆에 붙어있어야 하므로 (N * 2) + 2 의 인덱스를 가질 것이다

항목을 추가하거나 삭제하더라도 힙의 구조가 유지되어야 한다

class MinHeap extends Heap{
    constructor () {
        super();
        this.items = [];
    }

    add(item) {
        this.items[this.items.length] = item;
        this.bubbleUp();
    }

    poll() {
        let item = this.items[0];
        this.items[0] = this.items[this.items.length - 1];
        this.items.pop();
        this.bubbleDown();
        return item;
    }

    bubbleDown() {
        let index = 0;
        while (this.leftChild(index) && this.leftChild(index) < this.items[index]) {
            let smallerIndex = this.leftChildIndex(index);
            if (this.rightChild(index) && this.rightChild(index) < this.items[smallerIndex])
                smallerIndex = this.rightChildrenIndex(index);  
            this.swap(smallerIndex, index);
            index = smallerIndex;
        }
    }

    bubbleUp() {
        let index = this.items.length - 1;
        while(this.parent(index) && this.parent(index) > this.items[index]) {
            this.swap(this.parentIndeX(index), index);
            index = this.parentIndex(index);
        }
    }
}

최대 힙의 경우 최소 힙에서 구현한 bubbleDown과 bubbleUp 내 비교자 뿐이다

bubbleDown() {
    let index = 0;
    while (this.leftChild(index) && this.leftChild(index) > this.items[index]
            || this.rightChild(index) > this.items[index]) {
        let biggerIndex = this.leftChildIndex(index);
        if (this.rightChild(index) && this.rightChild(index) < this.items[biggerIndex])
            biggerIndex = this.rightChildrenIndex(index);  
        this.swap(biggerIndex, index);
        index = biggerIndex;
    }
}

bubbleUp() {
    let index = this.items.length - 1;
    while(this.parent(index) && this.parent(index) < this.items[index]) {
        this.swap(this.parentIndeX(index), index);
        index = this.parentIndex(index);
    }
}

힙 노드 인덱스 요약

노드	인덱스
자신	N
부모	(N - 1) / 2
왼쪽 자식	(N * 2) + 1
오른쪽 자식	(N * 2) + 2

힙은 삼투를 통해 자신의 구조를 유지한다(bubbleUp, bubbleDown)
이 삼투 과정이 있어 삭제와 삽입이 O(log2(n)) 시간에 가능해진다

일련의 숫자에서 중간 값을 찾기

/*
    하나의 최소 힙과 하나의 최대 힙을 만들면 중간 값을 얻는 데 O(1)시간이 걸림
*/

class MedianHeap {
    constructor() {
        this.minHeap = new MinHeap();
        this.maxHeap = new MaxHeap();
    }

    add(value) {
        if (value > this.median()) 
            this.minHeap.add(value);
        else 
            this.maxHeap.add(value);
        

        if (this.minHeap.size() - this.maxHeap.size() > 1) 
            this.maxHeap.add(this.minHeap.poll());
        
        if (this.maxHeap.size() - this.minHeap.size() > 1)
            this.minHeap.add(this.maxHeap.poll());
    }

    median() {
        if(this.minHeap.size() === 0 && this.maxHeap.size() === 0) 
            return Number.NEGATIVE_INFINITY;
        else if (this.minHeap.size() === this.maxHeap.size())
            return (this.minHeap.peek() + this.maxHeap.peek()) / 2;
        else if (this.minHeap.size() > this.maxHeap.size()) 
            return this.minHeap.peek();
        else 
            return this.maxHeap.peek();
    }
}

배열에서 K번째로 가장 작은/큰 값 찾기

let arr = [12, 3, 13, 4 ,2, 40, 23];
const getKthSmallestElement = (arr, k) => {
    let minH = new MinHeap();
    for (let i = 0, len = arr.length; i < len; i++) {
        minH.add(arr[i]);
    }
    
    for (let i = 1; i < k; i++) {
        minH.poll();
    }

    return minH.poll();
}

const getKthSmallestElement = (arr, k) => {
    let maxH = new MaxHeap();
    for (let i = 0, len = arr.length; i < len; i++) {
        maxH.add(arr[i]);
    }
    
    for (let i = 1; i < k; i++) {
        maxH.poll();
    }

    return maxH.poll();
}

17장 그래프

그래프를 사용하면 객체 간의 연결을 다양하게 나타낼 수 있다
그래프 기본 용어 및 개념

단어	뜻
정점	그래프를 형성하는 노드로 원으로 표기
간선	그래프에서 노드 간의 연결로 정점(원)사이의 선으로 표기
정점 차수	해당 점점에 연결된 간선의 개수
희소 그래프	정점들 간 가능한 연결 중 일부만 존재하는 경우
밀집 그래프	다양한 정점들 간에 연결이 많은 경우
순환 그래프	어떤 정점에서 출발해 해당 정점으로 다시 돌아오는 경로가 있는 지향성 그래프
가중치	간선에 대한 값으로 문맥에 따라 다양한 것을 나타냄(정점 간 거리 등)

무지향성 그래프는 간선 간에 방향이 없는 그래프로 노드 간 방향 없이 상호 연결을 뜻한다
인접 행렬과 인접 리스트를 사용하여 무지향성 그래프를 자료 구조 클래스로 표현할 수 있다

가중치가 있는 무지향성 그래프에 정점과 간선을 추가하기

class UndirectedGraph {
    constructor () {
        this.edges = {};
    }

    addVertext(vertex) {
        this.edges[vertex] = {};
    }

    addEdge(vertex1, vertex2, weight) {
        if (weight === undefined)
            weight = 0;
        this.edges[vertex1][vertex2] = weight;
        this.edges[vertex2][vertex1] = weight;
    }

    removeEdge(vertex1, vertex2) {
        if (this.edges[vertex1] && this.edges[vertex1][vertex2] !== undefined) 
            delete this.edges[vertex1][vertex2]
        if (this.edges[vertex2] && this.edges[vertex2][vertex1] !== undefined)
            delete this.deges[vertex2][vertex1]
    }

    removeVertex = function(vertex) {
        for (let adjacentVertex in this.edges[vertex]) {
            this.removeEdge(adjacentVertex, vertex);
        }
        delete this.edges[vertex];
    }
}

정점간에 방향이 있는 지향성 그래프를 구현하기

class DirectedGraph {
    constructor() {
        this.edges = {};
    }

    addVertex(vertex) {
        this.edges[vertex] = {};
    }

    addEdge(origVertex, destVertex, weight) {
        if(weight === undefined)
            weight = 0;

        this.edges[origVertex][destVertex] = weight;
    }

    removeEdge(origVertex, destVertex) {
        if(this.edges[origVertex] && this.edges[origVertex][destVertex] !== undefined)
            delete this.deges[origVertex][destVertex];
    }

    removeVertex(vertex) {
        for (let adjacentVertex in this.edges[vertex])
            this.removeEdge(adjacentVertex, vertex);
        delete this.edges[vertex];
    }

    traverseBFS(vertex, fn) {
        let queue = [], visited = {};
        queue.push(vertex);

        while(queue.length) {
            vertex = queue.shift();
            if(!visited[vertex]) {
                visited[vertex] = true;
                fn(vertex);
                for (let adjacentVertex in this.edges[vertex]) {
                    queue.push(adjacentVertex);
                }
            }
        }
    }

    traverseDFS(vertex, fn) {
        let visited = {};
        this._traverseDFS(vertex, visited, fn);
    }

    _traverseDFS(vertex, visited, fn) {
        visited[vertex] = true;
        fn(vertex);
        for (let adjacentVertex in this.edges[vertex]) {
            if(!visited[adjacentVertex])
                this. _traverseDFS(adjacentVertex, visited, fn)
        }
    }
}

가중치가 있는 그래프와 최단 경로
다익스트라 알고리즘은 목적지에 도달하기 위해 각 단계에서 최단 경로를 취하는 방식으로 동작한다

처음에는 일부 노드에 도달할 수 없을 수도 있기 때문에 거리를 무한으로 표기한다

function _isEmpty(obj) {
    return Object.keys(obj).length === 0;
}

function _extractMin(Q, dist) {
    let minimumDistance = Infinity,
        nodeWithMinimumDistance = null;
    for (let node in Q) {
        if (dist[node] <= minimumDistance) {
            minimumDistance = dist[node];
            nodeWithMinimumDistance = node;
        }
    }
    return nodeWithMinimumDistance;
}
// class DirectedGraph 내부라고 가정
    Dijkstra(source) {
        let Q = {}, dist = {};
        for (let vertex in this.edges) {
            dist[vertex] = Infinity;
            Q[vertex] = this.edges[vertex];
        }
        dist[source] = 0;

        while (!_isEmpty(Q)) {
            let u = _extractMin(Q, dist);
            delete Q[u];

            for (var neighbor in this.edges[u]){
                let alt = dist[u] + this.edges[u][neighbor];
                if (alt < dist[neighbor]) 
                    dist[neighbor] = alt;
            }
        }
        return dist;
    }

위상 정렬 알고리즘은 순서를 기록하기 위해 스택을 사용하는 수정된 버전의 깊이 우선 정렬

이 알고리즘은 어떤 노드로부터 깊이 우선 정렬을 수행해 해당 노드와 연결된 모든 노드들을 재귀적으로 방문하면서 해당 노드들을 스택에 추가한다

// class DirectedGraph 내부라고 가정
    topologicalSortUtil(v, visited, stack) {
        visited.add(v);
        for (let item in this.edges[v]){
            if (visited.has(item) === false) {
                this.topologicalSortUtil(item, visited, stack)
            }
        }
        stack.unshift(v);
    }

    topologicalSort() {
        let visited = new Set(), stack = [];

        for (let item in this.edges) {
            if (visited.has(item) === false) {
                this.topologicalSortUtil(item, visited, stack);
            }
        }
        return stack;
    }

Comment and share

21-03-13 자바스크립트로 하는 자료구조와 알고리즘(8)

Mar 13, 2021 in 알고리즘, 서적

15장 트리

이진 트리는 자식 노드가 왼쪽과 오른쪽뿐인 트리이다

class BinaryTreeNode {
  constructor (value) {
    this.value = value;
    this.left = null;
    this.right = null;
  }
}

class BinaryTree {
  this._root = null;
}

트리를 순회하려면 인덱스를 사용해 트리에 접근한 다음 크기 제한에 도달할 때까지 인덱스를 증가한다

선순위, 후순위, 중순위, 단계순위 순회 등이 있다

// 선순위
  traversePreOrder () {
    traversePreOrderHelper(this._root);

    function traversePreOrderHelper(node) {
      if(!node) return;
      console.log(node.value);
      traversePreOrderHelper(node.left);
      traversePreOrderHelper(node.right);
    }
  }

  traversePreOrderInterative() {
    let nodeStack = [];
    nodeStack.push(this._root);

    /*
    1) 항목을 출력
    2) 오른쪽 자식을 스택에 추가
    3) 왼쪽 자식을 스택에 추가
    스택구조이므로 오른쪽을 먼저 넣고 왼쪽을 나중에 넣음 (pop으로 꺼내면 왼쪽이 먼저 처리됨)
    */
    while (nodeStack.length) {
      let node = nodeStack.pop();
      console.log(node.value);
      if(node.right) nodeStack.push(node.right);
      if(node.left) nodeStack.push(node.left);
    }
  }

// 중순위
  traverseInOrder() {
    traverseInOrderHelper(this._root);

    function traverseInorderHelper(node) {
      if(!node) return;
      traverseInOrderHelper(node.left);
      console.log(node.value);
      traverseInOrderHelper(node.right);
    }
  }

  traverseInOrderInterative() {
    let current = this._root,
        s = [],
        done = false;
    
    while (!done) {
      // 현재 노드의 가장 왼쪽에 있는 노드로 이동
      if (current != null) {
        // 왼쪽 하위 트리를 순회하기 전에 포인터가 스택의 트리 노드를 가리키도록 함
        s.push(current);
        current = current.left
      } else {
        if(s.length) {
          current = s.pop();
          console.log(current.value);
          current = current.right;
        } else {
          done = true;
        }
      }
    }
  }

// 후순위
  traversePostOrder() {
    traversePostOrderHelper(this._root);

    function traversePostOrderHelper(node) {
      if (node.left) 
        traversePostOrderHelper(node.left)
      if (node.right)
        traversePostOrderHelper(node.right)
      console.log(node.value);
    }
  }

  traversePostOrderInterative() {
    let s1 = [], s2 = [];
    s1.push(this._root);
    while(s1.length) {
      let node = s1.pop();
      s2.push(node)

      if (node.left) 
        s1.push(node.left);
      if (node.right) 
        s1.push(node.right);
    }
    while(s2.length) {
      let node = s2.pop();
      console.log(node.value);
    }
  }
// 단계순위 순회
  traverseLevelOrder() {
    let root = this._root, queue = [];
    if(!root) return;
    queue.push(root);
    
    while(queue.length) {
      let temp = queue.shift();
      console.log(temp.value);
      if(temp.left) queue.push(temp.left);
      if(temp.right) queue.push(temp.right);
    }
  }

리프 노드를 방문하기 전에 루트를 조사할 필요가 있는 경우 선순위 순회 를 선택
리프 노드를 검색할 때 루트를 조사하느라 시간을 낭비하기 싫다면 후순위 순회 를 선택
트리를 원래 순서대로 방문하고 싶은 경우에는 중순위 순회 를 선택
이진 검색 트리의 경우 왼쪽 자식이 부모보다 작고 오른쪽 자식이 부모보다 크다

자식이 부모 값보다 큰 노드만 있는 경우 불균형 이진 검색트리가 되고 이 트리는 완전 균형 이진 트리에 비해 복잡도가 O(log2n)에서 O(n)으로 늘어난다

class BinarySearchTree {
  constructor () {
    this._root = null;
  }

  insert(value) {
    let thisNode = { left : null, right : null, value: value};
    if (!this._root) {
      this._root = thisNode;
    } else {
      let curRoot = this._root;
      while(true) {
        if (curRoot.value > value) {
          // 현재 노드보다 값이 작다면 왼쪽에 삽입
          if (curRoot.left != null) {
            curRoot = curRoot.left;
          } else {
            curRoot.left = thisNode;
            break;
          }
        } else if (curRoot.value < value) {
          // 현재 노드보다 값이 크면 오른쪽에 삽입
          if (curRoot.right != null) {
            curRoot = curRoot.right;
          } else {
            curRoot.right = thisNode;
            break;
          }
        } else {
          // 현재 노드와 값이 같을 경우
         break; 
        }
      } 
    }
  } // insert() end

  /*
    삭제하고자 하는 노드를 찾기 위해 트리를 순회해야 한다
    노드에 자식이 없을 경우에는 null을 반환하고 해당 노드를 삭제하면 된다
    노드에 자식이 하나 있다면 현재 자식을 반환하고 해당 자식이 위 단계로 올라가서 부모를 대체해야 한다
    노드에 자식이 두개 있다면 왼쪽 하위 트리의 최대치를 찾거나 오른쪽 하위 트리 최소치를 찾아서 해당 노드를 대체한다
  */
  remove (value) {
    return deleteRecursively(this._root, value);

    function deleteRecursively(root, value) {
      if (!root) {
        return null;
      } else if (value < root.value) {
        root.left = deleteRecursively(root.left, value);
      } else if (value > root.value) {
        root.right = deleteRecursively(root.right, value);
      } else {
        if (!root.left && !root.right) { 
          return null;
        } else if (!root.left) {
          root = root.right;
          return root;
        } else if (!root.right) {
          root = root.left;
          return root;
        } else {
          let temp = findMin(root.right);
          root.value = temp.value;
          root.right = deleteRecursively(root.right, temp.value)
          return root;
        }
      } 
      return root;
    }

    function findMin(root) { // 이진트리에서 가장 왼쪽에 있는 값은 최소값이다
      while(root.left) {
        root = root.left;
      }
       return root;
    }
  } // remove() end

  findNode(value) {
    let curRoot = this._root,
        found = false;

    while (curRoot) {
      if (curRoot.value > value) {
        curRoot = curRoot.left
      } else if (curRoot.value < value) {
        curRoot= curRoot.right
      } else {
        found = true;
        break;
      }
    }
    return found;
  }
}

AVL 트리는 스스로 균형을 잡는 이진 검색 트리로, 트리의 높이를 최소로 유지하면서 검색과 삽입, 삭제 연산의 시간 복잡도 O(log2(n))을 보장한다

class AVLTree {
  constructor (value) {
    this.left = null;
    this.right = null;
    this.value = value;
    this.depth = 1;
  }
  
  setDepthBasedOnChildren() {
    if (this.node === null) this.depth = 1;

    if (this.left !== null) this.depth = this.left.depth + 1;

    if (this.right !== null && this.depth <= this.right.depth) {
      this.depth = this.right.depth + 1;
    }
  }
  // 삽입 이후에 균형을 유지하기 위해 자식들을 회전
  rotateRR() {
    let valueBefore = this.value;
    let leftBefore = this.left;
    this.value = this.right.value;

    this.left = this.right;
    this.right - this.right.right;
    this.left.right = this.left.left;
    this.left.left = leftBefore;
    this.left.value = valueBefore;

    this.left.setDepthBasedOnChildren();
    this.setDepthBasedOnChildren();
  }

  rotateLL() {
    let valueBefore = this.value;
    let rightBefore = this.right;
    this.value = this.left.value;

    this.right = this.left;
    this.left - this.left.left;
    this.right.left = this.right.right
    this.right.right = rightBefore;
    this.right.value = valueBefore;

    this.right.setDepthBasedOnChildren();
    this.setDepthBasedOnChildren();
  }

  // 만약 한번 회전을 하고 나서도 AVL 트리가 여전히 불균형이라면 완전한 균형을 위해 두 번 회전해야 함 
  balance() {
    let ldepth = this.left === null ? 0 : this.left.depth;
    let rdepth = this.right === null ? 0 : this.right.depth;
    
    if (ldepth > rdepth + 1) {
      let lldepth = this.left === null ? 0 : this.left.depth;
      let lrdepth = this.right === null ? 0 : this.right.depth;

      if (lldepth < lrdepth) {
        // LR 회전은 왼쪽 자식의 RR회전과 현재 노드의 LL회전으로 구성된다
        this.left.rotateRR();
      }
      this.rotateLL();
    } else if (ldepth + 1 < rdepth) {
      let rrdepth = this.right.right === null ? 0 : this.right.right.depth;
      let rldepth = this.right.left === null ? 0 : this.right.left.depth;

      if (rldepth > rrdepth) {
        // RR회전은 오른쪽 자식의 LL회전과 현재 노드의 RR회전으로 구성됨
        this.right.rotateLL();
      }
      this.rotateRR();
    }
  } // balance() end

  insert (value) {
    let childInserted = false;
    if (value === this.value) {
      return false;
    } else if (value < this.value) {
      if (this.left === null) {
        this.left = new AVLTree(value);
        childInserted = true;
      } else {
        childInserted = this.left.insert(value);
        if (childInserted === true) this.balance();
      }
    } else if (value > this.value) {
      if (this.right === null) {
        this.right = new AVLTree(value);
        childInserted = true;
      } else {
        childInserted = this.right.insert(value);
        if(childInserted === true) this.balance();
      }
    }
    if (childInserted === true) this.setDepthBasedOnChildren();
    return childInserted;
  } // insert() end

  remove(value) {
    return deleteRecursively(this, value);

    function deleteRecursively(root, value) {
      if (!root) {
        return null;
      } else if (value < root.value) {
        root.left = deleteRecursively(root.left, value);
      } else if (value > root.value) {
        root.right = deleteRecursively(root.right, value);
      } else {
        if (!root.left && !root.right) {
          return null;
        } else if (!root.left) {
          root = root.right;
          return root;
        } else if (!root.right) {
          root = root.left;
          return root;
        } else {
          let temp = findMin(root.right);
          root.value = temp.value;
          root.right = deleteRecursively(root.right, temp.value);
          return root;
        }
      }
      root.setDepthBasedOnChildren();
      return root;
    }

    function findMin(root) {
      while (root.left) root = root.left;
      return root;
    }
  } // remove() end
}

이진 검색 트리는 검색에는 매우 뛰어나지만 삽입과 삭제의 연산 시간 복잡도가 O(log2(n))으로 느림
트리가 불균형이 되면 모든 연산이 O(n)이 되니 이를 개선하기 위해 AVL 트리와 같은 자가 균형 트리를 사용해야 한다

주어진 이진트리에서 두 개의 노드의 가장 가까운 공통 조상 찾기

function findLowestCommonAncester(root, value1, value2) {
  function findLowestCommonAncesterHelper(root, value, value2) {
    if (!root) return;
    if (Math.max(value1, value2) < root.value)
      return findLowestCommonAncesterHelper(root.left, value1, value2);
    if (Math.min(value1, value2) > root.value)
      return findLowestCommonAncesterHeleper(root.right, value1, value2);
    return root.value;
  }
  return findLowestCommonAncesterHelper(root, value1, value2);
}

루트의 n번째 거리에 있는 노드 출력하기

const printKthLevels = (root, k) => {
  let arrayKth = [], queue = [];

  if (!root) return;

  queue.push([root, 0]);

  while(queue.length) {
    let tuple = queue.shift(),
        temp = tuple[0];
        height = tuple[1];
    if (height === k) {
      arrayKth.push(temp.value);
    }
    if (temp.left) 
      queue.push([temp.left, height+1]);
    if (temp.right)
      queue.push([temp.right, height+1]);
  }
  console.log(arrayKth);
}

이진 트리가 다른 트리의 하위 트리인지 확인하기

const isSameTree = (root1, root2) => {
  if (root1 === null && root2 === null) return true;
  if (root1 === null || root2 === null) return false;

  return root1.value === root2.value 
    && isSameTree(root1.left, root2.left) 
    && isSameTree(root1.right, root2.right)
}

const checkIfSubTree = (root, subtree) => {
  let queue = [], counter = 0;

  if(!root) return;

  queue.push(root);

  while (queue.length) {
    let temp = queue.shift();
    if (temp.data === subtree.data === isSameTree(temp, subtree)) {
      return true
    }
    if (temp.left)
      queue.push(temp.left);
    if (temp.right)
      queue.push(temp.right);
  }
  return false;
}

트리가 다른 트리와 대칭인지 확인하기

/*
1. 두 트리의 루트 노드 키가 동일해야 함
2. 트리 a의 루트 왼쪽 하위 트리와 트리 b의 오른쪽 하위 트리가 대칭
3. 트리 a의 오른쪽 하위 트리와 트리 b의 왼쪽 하위 트리가 대칭
*/

const isMirrorTrees = (tree1, tree2) => {
  // 기저의 경우 둘 다 빈 상태
  if (!tree1 && !tree2) return true;
  // 둘 중 하나가 빈 상태라면 대칭이 아님
  if (!tree1 || !tree2) return false;

// 한쪽 트리의 왼쪽 하위 트리와 다른 트리의 오른쪽 하위 트리를 전달
  let checkLeftwithRight = isMirrorTrees(tree1.left, tree2.right),
      checkRightwithLeft = isMirrorTrees(tree2.right, tree1.left);
  return tree1.value === tree2.value && checkLeftwithRight && checkRightwithLeft;
}

Comment and share

21-03-12 자바스크립트로 하는 자료구조와 알고리즘(7)

Mar 12, 2021 in 알고리즘, 서적

13장 연결 리스트

연결 리스트란 각 노드가 달느 노드를 가리키는 자료구조이다
고정된 크기를 갖는 배열과는 달리 실행 시간에 메모리를 할당하거나 해제할 수 있는 동적 자료구조

연결 리스트 자료구조는 각 노드가 다음 노드에 대한 참조를 갖는 자료구조로 data와 next속성이 있다

class SinglyLinkedListNode {
  constructor (data) {
    this.data = data;
    this.next = null; // 노드 마지막 연결지점은 null값임
  }
}

class SinglyLinkedList {
  constructor () {
    this.head = null;
    this.size = 0;
  }

  isEmpty() {
    return this.size === 0;
  }
}

연결 리스트의 시작을 헤드라고 부르고 이 값은 아무 항목도 삽입되지 않으면 null이다

연결 리스트의 헤드가 비어있는 경우엔 신규 노드로 설정되고 비어있지 않다면 예전 헤드가 temp에 저장된 후에 새로운 헤드가 신규로 추가된 노드가 된다

// 위에서 이어짐
  insert(value) {
    if (this.head === null) this.head = new SinglyLinkedListNode(value);
    else {
      let temp = this.head;
      this.head = new SinglyLinkedListNode(value);
      this.head.next = temp;
    }
    this. size++;
  }

단일 연결 리스트에서 노드를 삭제하는 것은 해당 노드의 참조를 제거함으로써 구현할 수 있다

next가 가리키는 노드를 찾고 해당 노드의 next 주소값을 이전 노드의 next값으로 할당하면 노드를 삭제할 수 있다

remove(value) {
  let currHead = this.head;
  if (currHead.data === value) {
    // 삭제하고자 하는 노드가 지금 데이터와 같다면 헤드를 다음 노드로 변경하고 사이즈를 줄임
    this.head = currHead.next;
    this.size--;
  } else {
    // 헤드를 prv로 저장하고
    let prev = currHead;
    while (currHead.next) {
      // next 주소값이 null이 아닐때까지 순회한다
      if (currHead.data === value) {
        // 해당 값을 찾았다면 이전 값의 next를 현재 값의 next로 변경 (중간 잘라냄)
        prev.next = currHead.next;
        // prev값을 지금 head로 변경
        prev = currHead;
        currHead = currHead.next;
        break;
      }
      prev = currHead;
      currHead = currHead.next;
    }

    if (currHead.data === value) {
      // 삭제하는 노드의 next 주소값은 null로 변경하여 잘라내기
      prev.next = null;
    }

    this.size--;
  }
}

연결 리스트의 헤드에 있는 항목을 삭제하는 것은 O(1)만에 가능한데 맨 처음에 있는 값이기 때문

deleteHead() {
  let toReturn = null;

  if (this.head !== null) {
    toReturn = this.head.data;
    this.head = this.head.next;
    this.size--;
  }
  return toReturn;
}

연결 리스트 내의 값을 검색하려면 모든 next 포인터를 반복순회해야한다

find (value) {
  let currHead = this.head;
  while(currHead.next) {
    if (currHead.data === value) {
      return true;
    }
    currHead = currHead.next;
  }
  return false;
}

이중 연결 리스트는 양방향 단일 연결 리스트 같은 것이다

class DoubleLinkedListNode {
  constructor (data) {
    this.data = data;
    this.next = null;
    this.prev = null;
  }
}

class DoubleLinkedList {
  constructor () {
    this.head = null;
    this.tail = null;
    this.size = 0;
  }

  isEmpty () {
    return this.size === 0;
  }
}

양방향으로 연결되어 있으므로 노드들은 next와 prev 둘 다 갖는다

헤드에 항목을 삽입하는 것은 prev 포인터를 갱신해야 한다는 점 빼고는 단일 연결 리스트와 같다

insertHead (value) {
  if (this.head === null) {
    // 헤드가 비어있다면 이 헤드에 새로운 값을 갖는 노드를 추가
    this.head = new DoublyLinkedListNode(value);
    this.tail = this.head;
    // 단 하나만 있을 경우에 이 노드가 헤드이자 테일이기 때문
  } else {
    // 이미 헤드가 있다면 임시로 노드를 만들고
    let temp = new DoublyLinkedListNode(value);
    // 만든 노드의 next값을 현재 헤드값으로 변경하고
    temp.next = this.head;
    // 현재 헤드값의 prev값을 새로 만든 노드로 설정한다 (양방향이므로)
    this.head.prev = temp;
    // 새로 만든 노드가 새 헤드가 된다 (있었던 헤드가 밀려남)
    this.head = temp;
  }
  this.size++;
}

헤드를 삭제할 때 연결 리스트가 하나의 노드라면 prev와 next 모두 null로 설정해야 하며 여러개 존재하는 경우 삭제하는 헤드의 next값을 헤드로 설정한다

신규 헤드의 prev값을 null로 설정하여 참조를 제거한다

deleteHead () {
  let toReturn = null;
  if (this.head !== null) {
    toReturn = this.head.data;

    if (this.tail === this.head) {
      this.head = null;
      this.tail = null;
    } else {
      this.head = this.head.next;
      this.head.prev = null;
    }
  }
  this.size--;
  return toReturn; // dequeue와 같은 방식임 
}

테일 항목 삭제도 헤드 삭제와 같은 방식으로 제거한다

deleteTail() {
  let toReturn = null;

  if(this.tail !== null) {
    toReturn = this.tail.data;

    if (this.tail === this.head) {
      this.head = null;
      this.tail = null;
    } else {
      this.tail = this.tail.prev;
      this.tail.next = null;
    }
  } 
this.size--;
return toReturn;
}

양항향 연결 리스트에서는 헤드에서 헤드의 next 포인터를 사용할 수 있다 (반대로도 가능)

findFromHead (value) {
  let currHead = this.head;
  while (currHead.next) {
    if (currHead.data === value) return true;
    currHead = currHead.next;
  }
  return false;
}

단일 연결 리스트 뒤집기

const reverseSinglyLinkedList = sll => {
  let node = sll.head;
  let prev = null;
  // 방향성을 반대로 바꾸는 과정
  while (node) {
    let temp = node.next;
    node.next = prev;
    prev = node;
    if (!temp) break;
    node = temp;
  }
  return node;
}

연결 리스트에서 중복된 항목 제거하기

const deleteDuplicateDataInSLL = sll => {
  let track = [];

  let temp = sll.head;
  let prev = null;
  while (temp) {
    if (track.indexOf(temp.data) >= 0) {
      prev.next = temp.next;
      sll.size--;
    } else {
      track.push(temp.data);
      prev = temp;
    }
    temp = temp.next;
  }
  console.log(temp);
}

개선하기

const deleteDuplicateDataInSLL = sll => {
  let track = {};
  let temp = sll.head;
  let prev = null;
  while (temp) {
    if(track[temp.data]) {
      prev.next = temp.next;
      sll.size--;
    } else {
      track[temp.data] = true;
      prev = temp;
    }
    temp = temp.next;
  }
  console.log(temp);
}

14장 캐싱

캐싱은 자료를 임시 메모리에 저장하는 과정으로 대표적인 캐싱 방법에는 LFU(Least Frequently Used) 캐싱과 LRU(Least Recently Used) 캐싱이 있다
최근에 접근한 메모리 위치를 다시 접근할 가능성이 높고(시간적 지역성), 최근에 접근한 메모리 위치 주변의 위치를 다시 접근할 가능성이 높다(공간적 지역성)
LFU 캐싱은 운영체제가 메모리를 관리하기 위해 사용하는 캐싱 알고리즘으로 가장 참조 빈도가 낮은 항목을 삭제한다
LFU 캐시는 이중 연결 리스트를 사용해 O(1)시간에 항목을 제거한다

LFU의 노드에는 freqCount 속성이 있다

class LFUNode {
  constructor (key, value) {
    this.prev = null;
    this.next = null;
    this.key = key;
    this.data = data;
    this.freqCount = 1;
  }
}

class LFUDoublyLinkedList {
  constructor () {
    this.head = new LFUNODE('buffer head', null);
    this.tail = new LFUNODE('buffer tail', null);
    this.head.next = this.tail;
    this.tail.prev = this.head;
    this.size = 0;
  }

  insertHead (node) {
    node.next = this.head.next;
    this.head.next.prev = node;
    this.head.next = node;
    node.prev = this.head;
    this.size++;
  }

  removeTail () {
    let oldTail = this.tail.prev;
    let prev = this.tail.prev;
    prev.prev.next = this.tail; // 전 전 노드의 next를 테일로 지정
    this.tail.prev = prev.prev; // 테일을 제거하면 테일 앞 값을 테일로 지정해주어야 함
    this.size--;
    return oldTail;
  }

  removeNode(node) {
    node.prev.next = node.next;
    node.next.prev = node.prev;
    this.size--;
  }
  /*
    LFU의 set을 구현하기 위해서는 신규 항목의 삽입과 예전 항목의 교체가 필요함
    신규 항목을 삽입할 때 신규 노드가 생성되고 캐시 capacity가 꽉차지 않았다면 freq의 빈도 이중 연결 리스트에 삽입할 수 있다
    캐시가 꽉 찬 경우 빈도 이중 연결 리스트의 테일 항목이 삭제된 다음 삽입된다
  */
  set(key, value) {
    let node = this.keys[key];
    if (node === undefined) {
      node = new LFUNode(key, value);

      this.keys[key] = node;
      
      if (this.size !== this.capacity) {
        if (this.freq[1] === undefined) {
          this.freq[1] = new LFUDoublyLinkedList();
        }
        this.freq[1].insertHead(node);
        this.size++
      } else {
        let oldTail = this.freq[this.minFreq].removeTail();
        delete this.keys[oldTail.key];

        if (this.freq[1] === undefined) {
          this.req[1] = new LFUDoublyLinkedList();
        }

        this.freq[1].insertHead(node);
        this.minFreq = 1;
      } else {
        let oldFreqCount = node.freqCount;
        node.data = value;
        node.freqCount++;

        this.freq[oldFreqCount].removeNode(node);

        if (this.freq[node.freqCount] === undefined) {
          this.freq[node.freqCount] = new LFUDoublyLinkedList();
        } 

        this.freq[node.freqCount].insertHead(node);

        if (oldFreqCount === this.minFreq 
            && Object.keys(this.freq[oldFreqCount]).size === 0) {
              this.minFreq++;
        }
      }
    }
  }

  get (key) {
    let node = this.keys[key];

    if (node === undefined) return null;
    else {
      let oldFreqCount = node.freqCount;
      node.freqCount++;
      this.freq[oldFreqCount].removeNode(node);

      if (this.freq[node.freqCount] === undefined) {
        this.freq[node.freqCount] = new LFUDoublyLinkedList();
      }

      this.freq[node.freqCount].insertHead(node);

      if (oldFreqCount === this.minFreq 
          && Object.keys(this.freq[oldFreqCount]).length === 0) {
            this.minFreq++;
      }
      return node.data;
    }
  }
}

class LFUCache {
  constructor (capacity) {
    this.key = {}; // LFUNode를 저장하는 공간
    this.freq = {};// LFUDoublyLinkedList를 저장하는 공간
    this.capacity = capacity;
    this.minFreq = 0;
    this.size = 0;
  }
}

LRU 캐싱은 가장 오래된 항목을 먼저 제거하는 캐싱 알고리즘이다

캐시의 항목에 접근하면 해당 항목은 리스트의 뒤(가장 최신)로 이동하고 가장 앞에 있는 항목이 제거되며 새 항목은 가장 뒤에 추가된다

class DLLNode {
  constructor (key, data) {
    this.key = key;
    this.data = data;
    this.next = null;
    this.prev = null;
  }
}

class LRUCache {
  constructor (capacity) {
    this.keys = {};
    this.capacity = capacity;
    this.head = new DLLNode('', null);
    this.tail = new DLLNode('', null);
    this.head.next = this.tail
    this.tail.prev = this.head;
  }

  removeNode (node) {
    let prev = node.prev,
        next = node.next;
    prev.next = next;
    next.prev = prev;
  }

  addNode (node) {
    let realTail = this.tail.prev;
    realTail.next = node;

    this.tail.prev = node;
    node.prev = realTail;
    node.next = this.tail;
  }

  get (key) {
    let node = this.keys[key];
    if (node === undefined) return null;
    else {
      this.removeNode(node);
      this.addNode(node);
      return node.data;
    }
  }

  set (key, value) {
    let node = this.keys[key];
    if (node) this.removeNode(node);

    let newNode = new DLLNode(key, value);

    this.addNode(newNode);
    this.keys[key] = newNode;

    if (Object.keys(this.keys).length > this.capacity) {
      let realHead = this.head.next;
      this.removeNode(realHead);
      delete this.keys[realHead.key];
    }
  }
}

대부분의 경우 LFU는 LRU보다 성능이 떨어진다 LFU는 특정 시점에 한해 자주 사용된 경우를 배제할 수 없기 때문

Comment and share

21-03-12 자바스크립트로 하는 자료구조와 알고리즘(6)

Mar 12, 2021 in 알고리즘, 서적

11장 해시테이블

해시 테이블은 키-값 쌍을 기반으로 자료를 얻을 수 있다
해시 테이블에는 put()과 get()의 두 함수가 있어 자료를 저장하고 얻어올 수 있다
localStorage는 해시 테이블에 기반한 자료구조로 모든 브라우저가 지원하는 기본 자바스크립트 객체이다
해시 테이블에서 가장 중요한건 해시 함수로 이 함수는 특정 키를 자료를 저장하는 배열의 인덱스로 변환한다
좋은 해시 함수는 동일한 키는 동일한 해시값을 생성해야 하며(결정성), 시간 복잡도는 O(1)이어야 하며(효율성) 배열 전체를 최대한 활용해야 한다(균일한 분배)
해싱의 첫번째 기법은 소수를 사용하는 것 이다
소수에 의한 모듈러는 고정된 크기에 대해 가장 균등한 분배를 보장한다
소수 모듈러로 나눈 나머지 값으로 인덱싱하는 해시 테이블에서 같은 값이 있다면 충돌이 일어나게 되는데 이를 회피하기 위하여 탐사 해싱 기법을 이용한다
선형 탐사는 만약 같은 키로 해싱된다면 그 다음 빈 곳을 찾아 해싱한다
이 때 get(key)함수를 사용한다면 충돌된 부분을 찾은 후에 해당 값을 찾고자 테이블을 순회한다
이차 탐사는 선형 탐사와는 달리 1씩 증가시키지 않고 완전 제곱을 사용하여 사용 가능한 인덱스에 키를 균등하게 분배한다
이차 해싱 함수를 사용해 원래 해싱 함수로부터 나온 결과를 한 번 더 해싱하면 키를 균일하게 분배할 수 있다

해시 테이블 구현 (교재에는 옛날 방식으로 구현되어 있어서 class 문법을 사용하였음)

class HashTable {
    constructor(size) {
      this.size = size;
      this.keys = this.initArray(size);
      this.values = this.initArray(size);
      this.limit = 0;
    }
  
    put(key, value) {
      if (this.limit >= this.size) 
        throw 'hash table is full';
  
        let hashedIndex = this.hash(key);
  
        while (this.keys[hashedIndex] != null) {
          hashedIndex++
          hashedIndex = hashedIndex % this.size;
        }
      this.keys[hashedIndex] = key;
      this.values[hashedIndex] = value;
      this.limit++
    }
    
    get(key) {
      let hashedIndex = this.hash(key);
  
      while (this.keys[hashedIndex] != key) {
          hashedIndex++
          hashedIndex = hashedIndex % this.size;
      }
      return this.value[hashedIndex];
    }
    
    hash(key) {
      if(!Number.isInteger(key)) 
        throw 'must be number';
      return key % this.size;
    }
  
    initArray(size) {
      return Array.from({length: size}, () => null);
    }
}

이차 탐사 사용하기

class HashTable {
    constructor(size) {
      this.size = size;
      this.keys = this.initArray(size);
      this.values = this.initArray(size);
      this.limit = 0;
    }
  
    put(key, value) {
      if (this.limit >= this.size) 
        throw 'hash table is full';
  
        let hashedIndex = this.hash(key);
  
        while (this.keys[hashedIndex] != null) {
          hashedIndex++
          hashedIndex = hashedIndex % this.size;
        }
      this.keys[hashedIndex] = key;
      this.values[hashedIndex] = value;
      this.limit++
    }
    
    get(key) {
      let hashedIndex = this.hash(key);
  
      while (this.keys[hashedIndex] != key) {
          hashedIndex++
          hashedIndex = hashedIndex % this.size;
      }
      return this.value[hashedIndex];
    }
    
    hash(key) {
      if(!Number.isInteger(key)) 
        throw 'must be number';
      return key % this.size;
    }
  
    initArray(size) {
      return Array.from({length: size}, () => null);
    }
}

이차 탐사 (put, get 함수만)

put(key, value) {
  if (this.limit >= this.size) 
    throw 'hash table is full';
  
  let hashedIndex = this.hash(key), squareIndex = 1;
  
  while (this.keys[hashedIndex % this.size] != null) {
    hashedIndex += Math.pow(squareIndex, 2);
    squareIndex++;
  }
  this.keys[hashedIndex % this.size] = key
  this.value[hashedIndex % this.size] = value;
  this.limit++
}
    
get(key) {
  let hashedIndex = this.hash(key);
  
  while (this.keys[hashedIndex] != key) {
    hashedIndex++
    hashedIndex = hashedIndex % this.size;
  }
  return this.value[hashedIndex];
}

선형 탐사를 활용한 이중 해싱

put(key, value) {
  if (this.limit >= this.size) 
    throw 'hash table is full';
  
  let hashedIndex = this.hash(key);
  
  while (this.keys[hashedIndex] != null) {
    hashedIndex++;
    hashedIndex = hashedIndex % this.size;
  }
  this.keys[hashedIndex] = key
  this.value[hashedIndex] = value;
  this.limit++
}
    
get(key) {
  let hashedIndex = this.hash(key);
  
  while (this.keys[hashedIndex] != key) {
    hashedIndex++
    hashedIndex = hashedIndex % this.size;
  }
  return this.value[hashedIndex];
}

hash(key) {
  if (!Number.isInteger(key)) 
    throw 'must be number'
  return this.secondHash(key);
}

secondHash(hashedKey) {
  let R = this.size - 2;
  return R - hashedKey % R;
}

해시테이블은 크기가 처음에 정의되는(size를 매개변수로 생성자에 전달한 것을 보자) 고정된 크기의 자료구조이다
해시 함수를 사용해 균등하게 분배하고 충돌이 일어나는 것을 최대한 막아야한다

12장 스택과 큐

스택은 마지막에 삽입된 항목만을 제거하고 접근할 수 있다

자바스크립트에서 배열에는 스택 클래스를 정의한 pop과 push라는 메서드가 있다

class Stack {
  constructor (arr) {
    this.arr = [];
    if(arr) this.arr = arr;
  }

  getBuffer() {
    return this.arr.slice();
  }

  isEmpty() {
    return this.arr.length === 0;
  }

  peek() {
    return this.arr[this.arr.length-1];
  }

  push(value) {
    this.arr.push(value);
  }

  pop() {
    return this.arr.pop();
  }
}

위에서부터 n번째 노드에 접근하기 위해 pop을 n번 호출해야 한다

const stackAccessNthTopNode = (stack, n) => {
  let bufferArr = stack.getBuffer();
  if (n <= 0) throw 'error';

  let bufferStack = new Stack(bufferArr);

  while(--n! === 0) 
    bufferStack.pop();

  return bufferStack.pop();
}

검색 또한 이와 비슷한 방식으로 구현할 수 있다

const stackSearch = (stack, element) => {
  let bufferArr = stack.getBuffer();
  let bufferStack = new Stack(bufferArr);
  while(!bufferStack.isEmpty()){
    if (bufferStack.pop() === element) return true;
  }
  return false;
}

큐는 스택과 달리 첫번째로 추가도니 항목만을 제거할 수 있는 자료 구조이다
자바스크립트에서는 shift()와 push()라는 메서드가 있어 이 함수를 호출하면 배열의 첫번째 항목을 제거해 리턴한다

큐에 추가하는 것을 인큐(enqueuing)라고, 제거하는 것을 디큐(dequeuing)라 한다

class Queue {
  constructor (arr) {
    this.arr = [];
    if(arr) this.arr = arr;
  }

  getBuffer() {
    return this.arr.slice();
  }

  isEmpty() {
    return this.arr.length === 0;
  }

  peek() {
    return this.arr[0]; // 제거하지 않고 값만 리턴
  }

  enqueue(value) {
    return this.arr.push(value);
  }

  dequeue() {
    return this.arr.shift();
  }
}

큐에 접근할 때엔 인덱스로 접근할 수 없다 n번째 노드에 접근하려면 디큐를 n번 호출해야 한다

const queueAccessNthTopNode = (queue, n) => {
  let bufferArr = queue.getBuffer();
  if (n <= 0) throw 'error'

  let bufferQueue = new Queue(bufferArr);

  while(--n !== 0) 
    bufferQueue.dequeue(); // 필요한 노드 직전까지 디큐

  return bufferQueue.dequeue(); // 리턴으로 디큐하면 해당 노드가 필요한 노드
}

스택을 사용해 큐를 구현하기
→ 두개의 스택을 사용한다면 큐를 만들 수 있다

class TwoStackQueue {
  constructor() {
    this.inbox = new Stack();
    this.outbox = new Stack();
  }

  enqueue(value) {
    this.inbox.push(value);
  }

  dequeue() {
    if(this.outbox.isEmpty()) {
      while(!this.inbox.isEmpty()){
        this.outbox.push(this.inbox.pop());
      }
    }
    return this.outbox.pop();
  }
}

큐를 사용해 스택을 구현하기도 마찬가지로 두 개의 큐를 사용하면 스택을 구현할 수 있다

class QueueStack {
  constructor() {
    this.inbox = new Queue();
  }

  push(value) {
    this.inbox.enqueue(value);
  }

  pop() {
    let size = this.inbox.arr.length - 1;
    let cnt = 0;
    let bufferQueue = new Queue();
    while(++counter <= size)
      bufferQueue.enqueue(this.inbox.dequeue());
    let popped = this.inbox.dequeue();
    this.inbox = bufferQueue;
    return popped;
  }
}

고객 객체를 매개변수로 받아 선입선출(Queue) 방식으로 음식을 주문 처리하는 점원 클래스를 설계

점원은 주문을 위해 고객의 이름과 주문 항목을 요구

첫번째로 받은 주문을 먼저 처리함

class Customer {
  constructor (name, order) {
    this.name = name;
    this.order = order;
  }

  addOrder (customer) {
    this.customers.enqueue(customer);
  }

  deliverOrder() {
    let finishedCustomer = this.customers.dequeue();
  }
}

function Cashier() {
  this.customers = new Queue();
}

스택을 사용해 괄호 검증기를 설계하기

const BracketVerification = string => {
  let stack = new Stack();
  for (let pos = 0; pos < string.length; pos++) {
    let currentChar = string.charAt(pos);
    if(currentChar === "("){
      stack.push(currentChar);
    } else if (currentChar ===")") {
      if(stack.isEmpty()) return false;
      stack.pop();
    }
  }
  return stack.isEmpty();
}

정렬 가능한 스택 설계하기

class sortableStack {
  constructor (size) {
    this.size = size;
    this.mainStack = new Stack();
    this.sortedStack = new Stack();
    for (let i = 0; i < this.size; i++) {
      this.mainStack.push(Math.floor(Math.random() * 11));
    }
  }

  sortStackDescending() {
    while(!this.mainStack.isEmpty()){
      let temp = this.mainStack.pop();
      while(!this.sortedStack.isEmpty && this.sortedStack.peek() <temp) {
        this.mainStack.push(this.sortedStack.pop());
      }
      this.sortedStack.push(temp)
    }
  }
}

Comment and share

21-03-11 자바스크립트로 하는 자료구조와 알고리즘(5)

Mar 11, 2021 in 알고리즘, 서적

9장 집합

집합이란 유한하고 구분되는 객체들의 그룹
자바스크립트에서는 Set이 기본으로 지원된다
let exampleSet = new Set();
Set의 주요 특징은 유일함을 확인 한다는 것이다(중복되는 항목은 허용되지 않음)
Set.delete는 boolean값을 리턴하며 항목을 삭제할 수 있게 하는 메서드이다
Set.has는 집합 내에 존재하는지 확인하며 .delete / .has는 모두 O(1)의 시간 복잡도를 갖는다

Set을 사용하여 교집합 구하기

const intersectSets = (setA, setB) => {
  let intersection = new Set();
  for (let element of setB) {
    if (setA.has(element)) {
      intersection.add(element)
    }
    return intersection
  }
} // O(n)

어떤 집합이 다른 집합의 모든 항목을 포함하는 경우에는 상위 집합이 된다

const isSuperSet = (setA, subSet) => {
  for (let element of subSet) {
    if(!setA.has(element))
      return false;
  }
  return true;
}

Set을 사용한다면 합집합도 쉽게 구현할 수 있다

const unionSet = (setA, setB) => {
  let union = new Set(setA);
  for (let element of setB) {
    union.add(element);
  }
  return union
}

Spread Operator를 사용한 방법

1
2
3

const unionSetWithSpreadOperator = (setA, setB) => {
  return new Set([...setA,...setB]);
}

차집합은 .delete로 구현할 수 있다

const differenceSet = (setA, setB) => {
  let differ = new Set(setA);
  for (let element of setB) {
    differ.delete(element);
  }
  return differ;
}

집합을 사용해 배열의 중복 항목을 확인하기

const checkDupl = arr => {
  let mySet = newSet(arr);
  return mySet.size < arr.length;
}

개별적인 배열들에서 유일한 값만을 반환하기

const uniqueList = (arr1, arr2) => {
  // arr1 뒤에 arr2 배열을 붙이고 Set을 사용해 유니크한 값만 남기기
  let mySet = new Set(arr1.concat(arr2));
  return Array.from(mySet);
}

10장 검색과 정렬

검색은 자료 구조의 항목들을 반복적으로 접근하는 것 , 정렬은 자료구조의 항목들을 순서대로 위치시키는 것

한 인덱스씩 순차적으로 접근하는 선형 검색

const linearSearch = (arr, n) => {
  for (let i = 0, len = arr.length; i < len; i++) {
    if (arr[i] === n) return true;
  }
  return false;
}

정렬된 자료라면 이진검색을 사용할 수 있다

const binarySearch = (arr, n) => {
  let lowIndex = 0, highIndex = arr.length;
  while (lowIndex <= highIndex) {
    let midIndex = Math.floor((lowIndex + highIndex)/2);
    if (arr[midIndex] === n) return midIndex;
    else if (n > arr[midIndex]) lowIndex = midIndex+1;
    else highIndex = midIndex-1;
    return -1;
  }
}

이진검색을 사용하려면 자료를 정렬해야함

버블 정렬은 전체 배열을 순회하며 두 항목을 비교하고 교체하는 작업을 반복한다

const swap = (arr, idx1, idx2) => {
  let temp = arr[idx1];
  arr[idx1] = arr[idx2];
  arr[idx2] = temp;
}

const bubbleSort = arr => {
  for (let i = 0, len = arr.length; i < len; i++) {
    for (let j = 0; j <= i; j++){
      if (arr[j] > arr[j+1]) {
        swap(arr, i, j)
      } 
    }
  }
  return arr;
} // for문을 두 번 사용하므로 O(n의 제곱)값이 된다

선택 정렬은 가장 작은 항목을 찾고 해당 항목의 배열의 현 위치에 삽입하는 식으로 동작한다

const selectionSort = items => {
  let len = items.length, min;
  for (let i = 0; i < len; i++) {
    min = i;
    for (j = i+1; j < len; j++){
      if(items[j] < items[min]) min = j;
      if (i != min) swap(items, i, min);
    }
  }
  return items;
}

삽입 정렬을 배열을 순차적으로 검색하면서 정렬되지 않은 항목들을 왼쪽으로 이동시킨다

const insertionSort = items => {
  let len = items.length, 
      value, // 지금 비교중인 값
      i, // 정렬 안된 부분
      j; // 정렬 된 부분
  for (let i = 0; i < len; i++){
    // 
    value = items[i];
    for (j = i-1; j > -1 && items[j] > value; j--) {
      items[j+1] = items[j]
    }
    items[j+1] = value;
  }
  return items
}

퀵 정렬은 기준점을 기준으로 배열을 나눠 모든 항목이 정렬될 때까지 과정을 반복하는 정렬법이다

이 방법은 분할 정복을 이용한 재귀법으로 처리되어 평균 O(nlog2(n))으로 처리되지만 최악의 경우(이미 정렬된 배열을 받을 경우) O(n의 제곱)값을 갖는다

const quickSort = arr => {
  return quickSortHelper(arr, 0, arr.length-1);
}

const quickSortHelper = (arr, left, right) => {
  let idx;
  if (arr.length > 1) {
    idx = partition(arr, left, right);
    if (left < idx - 1) quickSortHelper(arr, left, idx -1);
    if (idx < right) quickSortHelper(arr, idx, right)
  }
  return arr;
}

const partition = (arr, left, right) => {
  let pivot = arr[Math.floor((left+right)/2)] // 배열의 중간값을 탐색
  // 정렬하다보면 left는 계속 증가하고 right는 계속 감소하므로 
  // left값이 right값을 넘어가게 됨 (base condition)
  while (left <= right) {
    while(pivot > arr[left]) left++
    while(pivot < arr[right]) right++
    if (left <= right) {
      let temp = arr[left];
      arr[left] = arr[right];
      arr[right] = temp;
      left++;
      right--;
    } 
  }
  return left;
}

퀵정렬의 단점은 기준점을 항상 잘못 선택하는 경우 시간 복잡도가 O(n의 제곱)이 될 수 있다는 것

퀵선택(quick select)은 정렬되지 않은 목록에서 k번째로 작은 항목을 찾는 선택 알고리즘으로 퀵정렬과는 달리 한쪽만 재귀적으로 수행함

// 정렬되지 않은 목록에서 k번째로 작은 항목을 찾기
const quickSelect = (arr, low, high, k) => {
  let p = partition(arr, low, high);
  if (p == (k-1)) return A[p];
  else if (p > (k-1)) return quickSelect(arr, low, p-1, k);
}

const medianQuickSelection = arr => {
  return quickSelect(arr, 0, arr.length-1, Math.floor(array.length/2))
} // O(n)의 시간복잡도

병합 정렬는 각 배열에 하나의 항목이 존재할때까지 나누고 순서대로 연결함

const merge = (leftArr, rightArr) => {
  let results = [], leftIdx = 0, rightIdx = 0;
  while (leftIdx < leftArr.length && rightIdx < rightArr.length){
    if (leftArr[leftIdx] < rightArr[rightIdx]) {
      results.push(leftArr[leftIdx++]);
    } else {
      results.push(rightArr[rightIdx++]);
    }
  }
  let leftReamins = leftArr.slice(leftIdx), 
      rightRemains = rightArr.slice(rightIdx);
  return results.concat(leftReamains).concat(rightRemains);
}

// 재귀함수로 배열을 전부 길이 1인 배열로 쪼개고 merge로 합하고를 반복한다
const mergeSort = arr => {
  if (arr.length <2) return arr;

  let mid = Math.floor(arr.length/2),
      leftArr = arr.slice(0, mid),
      rightArr = arr.slice(mid);
  
  return merge(mergeSort(leftArr), mergeSort(rightArr))
}

계수 정렬은 값들을 비교하지 않기 때문에 O(k+n)시간 안에 수행된다

계수 정렬은 숫자에 대해서만 동작하고 특정 범위가 주어져야 한다

const countSort = arr => {
  let hash = {}, countArr =[];
  // 해시 테이블을 생성하고 해시 테이블에 해당 값의 갯수를 셈
  for (let i = 0, len = arr.length; i < len; i++) {
    if (!hash[arr[i]]) hash[array[i]] = 1;
    else hash[array[i]]++;
  }
  // 값의 숫자를 센 해시테이블에서 값을 꺼내고 그 수 만큼 push를 반복
  for (let key in hash) {
    for (let i = 0; i < hash[key]; i++) {
      countArr.push(parseInt(key));
    }
  }
  return countArr;
} // O(k+n) 시간 복잡도를 가짐

자바스크립트의 내장 정렬 함수인 sort는 기본 오름차순으로 정렬하고 arr.sort((a,b) => a-b)와 같이 사용한다

수학 라이브러리를 사용하지 않고 정수의 제곱근 함수 구하기

const sqrtIntNaive = num => {
  if (num === 0 || num === 1) return num;

  let idx = 1, square = 1;
  while (square < number) {
    if (square === number) return square;

    idx++;
    square = idx*idx;
  }
  return idx;
}

이진 검색 알고리즘을 이용한 정수의 제곱근 함수 구하기

const sqrtInt = num => {
  if (num === 0 || num === 1) return num;

  let start = 1, end = num, ans;
  
  while (start <= end) {
    let mid = parseInt((start+end)/2)
    if (mid * mid === num) return mid;
    if (mid * mid < num) {
      start = mid+1;
      ans = mid
    } else {
      end = mid -1
    }
  }
  return  ans;
} // O(log2(n))

배열의 두 항목을 더해서 주어진 수가 될 수 있는지 확인하기

const findTwoSum = (arr, sum) => {
  for (let i = 0, len = arr.length; i < len; i++) {
    for (let j = i+1; j < len; j++) {
      if (arr[i]+arr[j] === sum) return true
    }
  }
  return false
}

배열에서 단 한번만 등장하는 항목 찾기

const findOnlyOnce = (arr, low, high) => {
  if (low > high) return null; // 배열의 길이가 0일때는 널값을 리턴
  if (low === high) return arr[low]; // 길이가 1일때
  
  let mid = Math.floor((high+low)/2); // 절반값을 구하고
  
  if (mid % 2 === 0) {
    if (arr[mid] === arr[mid+1]) // 오른쪽과 비교
      return findOnlyOnce(arr, mid+2, high);
    else 
      return findOnlyOnce(arr, low, mid)
  } else {
    if (arr[mid] === arr[mid-1]) // 왼쪽과 비교 
      return findOnlyOnce(arr, mid+1, high);
    else 
      return findOnlyOnce(arr, low, mid-1);
  }
}

const findOnlyOnceHelper = arr => {
  return findOnlyOnce(arr, 0, arr.length);
}

문자열을 길이순으로 정렬하는 자바스크립트 정렬 비교 함수

1
2
3

const sortByStringLength = arr => {
  return arr.sort((a, b) => a.length - b.length)
}

단어 세기 목록 구현하기

const wordCnt = sentence => {
  let wordsArr = sentence.replace(/[.]/g, "").split(''),
      occurenceList = {}, answerList = {};

  for (let i = 0, wordsLen = wordsArr.length; i < wordsLen; i++) {
    let currWord = wordsArr[i];
    if (!occurenceList[currWord]) occurenceList[currWord] = 1;
    else occurenceList[currWord]++;
  }
  
  let arrTemp = [];
  for (let prop in occurenceList) {
    arrTemp.push([occurenceList[props], prop])
  }

  arrTemp.sort((a,b) => b[0] - a[0]);

  for (let i = 0, len = arrTemp.length; i < len; i++) {
    let curr = arrTemp[i];
    answerList[curr[1]] = curr[0];
  }
  return answerList;
}

Comment and share

NEWER POSTS
OLDER POSTS
page 3 of 7

크레인 인형뽑기 게임

다트 게임

폰켓몬

가장 큰 정사각형 찾기

다음 큰 숫자

올바른 괄호

기능개발

가장 큰 수

프린터

19장 동적 프로그래밍

20장 비트 조작

18장 고급 문자열

16장 힙

17장 그래프

15장 트리

13장 연결 리스트

14장 캐싱

11장 해시테이블

12장 스택과 큐

9장 집합

10장 검색과 정렬

Harry Kim