21-03-10 자바스크립트로 하는 자료구조와 알고리즘(4)

in 알고리즘, 서적

6장 자바스크립트 객체

  • 자바스크립트가 여러 용도로 사용될 수 있는 이유는 객체 덕분이다
  • 객체 상수 {} 또는 new Object()를 통해 객체를 생성할 수 있다
  • object.propertyName 또는 object[‘propertyName’]으로 접근할 수 있다
  • 프로토타입을 활용 상속은 자바스크립트의 유일한 상속방법이다
  • 자바스크립트는 동적이고 클래스는 새로운 함수 멤버를 이후에 필요할 때 추가할 수 있기 때문
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    const classExample = () => {
      this.array = [1,2,3,4,5];
      this.name = "JavaScript";
    }

    let example1 = new classExample();

    classExample.prototype.sayName = function() {
      console.log(this.name);
    }
    // 동적으로 생성된 객체에 함수를 추가할 수 없다
    // example1.prototype.sayName2 = function() {} 같은 것은 불가능
  • 객체의 속성들을 다른 범위에서도 직접 접근할 수 있다
  • 비공개 변수(캡슐화)를 흉내내려면 지역변수를 선언하고 해당 변수에 접근할 수 있는 getter(), setter()를 만들 수 있다
  • 객체에 속성을 추가하기
    1
    2
    3
    4
    let obj = {};
    obj.example = 'value';
    obj['example'] = 'change';
    // 어떤 식으로 접근하든 성능상의 차이는 없음

    7장 자바스크립트 메모리 관리

  • V8 자바스크립트 엔진 및 최신 자바스크립트 엔진에는 가비지 컬렉터가 있어 사용하지 않는 변수를 삭제한다
  • 객체에 대한 참조가 있다면 해당 참조는 메모리에 있는 것이고, 객체 내에 저장된 변수를 참조할 때엔 해당 객체 전체를 로딩한다
  • DOM 항목을 가리키는 변수가 이벤트 콜백 외부에 선언된 경우엔 해당 DOM 항목을 제거하더라도 메모리에 남게 된다
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    let one = document.getElementById('one');
    let two = document.getElementById('two');
    one.addEventListener('click', () => {
      two.remove();
      console.log(two); // 삭제 이후에도 two를 참조하게 되므로 메모리 누수가 발생한다
    })
    /*-------------------------------------*/
    let one = document.getElementById('one');
    one.addEventListener('click', () => {
      let two = document.getElementById('two'); 
      // 블록 내에서만 사용하도록 처리하면 메모리 누수를 줄일 수 있다
      two.remove();
    })
    /*-------------------------------------*/
    let one = document.getElementById('one');
    one.addEventListener('click', () => {
      let two = document.getElementById('two'); 
      // 블록 내에서만 사용하도록 처리하면 메모리 누수를 줄일 수 있다
      two.remove();
    })
    one.removeEventListener('click');
  • 객체가 window 전역 객체에 포함되는 경우에도 해당 객체는 메모리에 존재하므로 가능하면 전역 변수는 사용하지 않는 것이 좋다
  • 객체 내 하나의 속성만 필욯나 경우 전체 객체를 매개변수로 전달해서는 안된다
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    let test = { prop : 'test' }
    /* 이렇게 구현해서는 안된다
    const printProp = (test) => {
      console.log(test.prop)
    } 
    */ 
    const printProp = prop => {
      console.log(prop)
    }
    printProp(test.prop);
  • 원치 않는 객체 속성은 delete 연산자로 제거할 수 있다 (객체가 아니라면 작동하지 않는다)
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    const colorCount = arr => {
      // 함수 밖에서 선언하면 메모리 낭비가 되므로 안에 선언해주자
      let RED = 0, GREEN = 1, BLUE = 2;
      let counter = new Array(3).fill(0);
      for (let i = 0, arrLen = arr.length; i < arrLen; i++) {
        let curr = arr[i];
        if (curr === RED) {
          counter[RED]++
        } else if (curr === GREEN) {
          counter[GREEN]++
        } else if (curr === BLUE) {
          counter[BLUE]++
        }
      }
      return counter;
    }

    8장 재귀

  • 재귀함수는 대개 분할 정복에 사용된다
  • 재귀함수를 사용하려면 점차 기저 조건 에 접근하는 분할 정복 방식 으로 구성하여야 한다
  • 피보나치 수열은 대표적인 예
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    // for문을 활용한 함수
    const getFibo = n => {
      if (n <= 1) return n;
      let sum = 0, last = 1, lastlast = 0;
      for (let i = 1; i < n; i++){
        sum = lastlast + last;
        lastlast = last;
        last = sum;
      }
      return sum;
    } 
    1
    2
    3
    4
    5
    const getFibo = n => {
      if (n <= 1) return n
      else return getFibo(n-1) + getFibo(n-2);
      // n-1 = last, n-2 = lastlast 인 셈
    }
  • 꼬리재귀를 이용한 구현
    1
    2
    3
    4
    5
    const getFiboBetter = (n, lastlast, last) => {
      if (n === 0) return lastlast;
      if (n === 1) return last;
      return getFiboBetter(n-1, last, lastlast + last)
    }
  • 파스칼의 삼각형
    1
    2
    3
    4
    5
    6
    const pascalTriangle = (row, col) => {
      if (col === 0) return 1;
      else if (row === 0) return 0;
      else 
        return pascalTriangle(row - 1, col) + pascalTriangle(row -1, col - 1);
    }
  • 삼항연산자를 이용한 파스칼의 삼각형
    1
    2
    3
    4
    5
    const pascalTriangle = (row, col) => {
        return (col === 0) ? 1 
                : (row === 0) ? 0 
                    : pascalTriangle(row - 1, col) + pascalTriangle(row -1, col - 1);
      }
  • 재귀의 빅오 분석은 점화식 을 분석해야한다
  • 이 점화식을 분석할 때 마스터 정리 를 자주 사용한다
    → T(n) = aT(n/b) + O(n^c) (단, a >= 1 , b >= 1)
    → a는 재귀호출에 곱해지는 계수이고 b는 로그 항임
    → 비재귀 요소인 O(n^c)의 c가 logb(a)보다 작다면 T(n) = O(n^3)
    → c가 logb(a)와 같은 경우엔 T(n) = O(nlog(n))
    → c가 logb(a)보다 크다면 T(n) = O(n^2)
  • 10진수를 2진수로 변환하기
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    // 1. base condition
    const base10ToString(n) {
      let binaryString ='';

      function base10ToStringHelper(n) {
        if (n < 2) {
          binaryString += n;
          return;
        } else {
          base10ToStringHelper(Math.floor(n/2));
          base10ToStringHelper(n%2);
        }
      }
      base10ToStringHelper(n);

      return binaryString;
    } // 시간 복잡도 O(log2(n));
  • 배열의 모든 순열 출력하기
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    // 1. base condition : beginIndex === endIndex;
    const swap = (strArr, index1, index2) => {
      let temp = strArr[index1];
      strArr[index1] = strArr[index2];
      strArr[index2] = temp;
    }

    const permute = (strArr, begin, end) => {
      if (begin === end) console.log(strArr);
      else {
        for (let i = begin; i < end + 1; i++){
          swap (strArr, begin, i);
          permute(strArr, begin + 1, end);
          swap(strArr, begin, i);
        }
      }
    }

    const permuteArray = strArr => {
      permute(strArr, 0, strArr.length - 1);
    }
  • 객체 펼치기
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    const dictionary = {
      'Key1' : '1',
      'Key2' : { 
        'a' : '2',
        'b' : '3',
        'c' : {
          'd' : '3',
          'e' : '1'
        }
      }
    }

    const flattenDictionary = dictionary => {
      let flattenedDictionary = {};

      function flattenDictionaryHelper (dictionary, propName) {
        if (typeof dictionary != 'object') {
          flattenedDictionalry[propName] = dictionary; 
          return;
        }
        for (let prop in dictionary) {
          if (propName === '') 
            flattenDictionaryHelper(dictonary[prop], propName+prop);
          else
            flattenDictionaryHelper(dictonary[prop], propName+'.'+prop)
        }
      }
      flattenDictionaryHelper(dictionary, '');
      return flattenedDictionary;
    } // 시간 복잡도 O(n)
  • 회문 검사하기
    1
    2
    3
    4
    5
    6
    7
    8
    9
    const isPalindrome = word => {
      return isPalindromeHelper(word, 0, word.length - 1);
    }

    const isPalindromeHelper = (word, beginPos, endPos) => {
      if (beginPos >= endPos) return true;
      if (word.charAt(beginPos) !== word.charAt(endPos)) return false
      else return isPalindromeHelper(word, beginPos + 1, endPos - 1);
    }

Comment and share

21-03-10 자바스크립트로 하는 자료구조와 알고리즘(3)

in 알고리즘, 서적

5장 자바스크립트 배열

  • 자바스크립트의 배열은 삽입, 삭제, 접근에 O(1) 복잡도를 갖는다
  • 삽입은 .push()나 .pop()을 사용해 배열 마지막에 추가하거나 삭제할 수 있다
  • array[1]과 같이 특정 인덱스에 접근한다면 메모리 주소로부터 직접 값을 얻어온다 (Java처럼 메모리 주소값을 알 수 있는 방법은 거의 없다, 스택오버플로우 참고)
  • n개의 항목을 방문하는 for문은 당연히도 O(n)의 시간 복잡도를 갖는다
  • while(true)와 같이 for( ; ;)로도 무한루프를 구현할 수 있다
  • for문은 for (index in arr) 이나 for (element of arr)와 같이 사용할 수 있다
  • 일반적인 for문과 달리 forEach는 배열의 각 요소에 대해 callback을 실행하므로 중간에 break할 수 없다 (MDN 참고)
  • 유용한 Array 내장함수
  1. .slice(begin, end) : 얕은 복사
    기존 배열을 수정하지 않고 배열의 일부분을 리턴하며 end값이 없다면 자동으로 맨 끝 인덱스로 가정한다
  2. .splice(begin, size, element1, element2…)
    첫 번째 매개변수에 지정한 값에 size만큼 잘라내고, 3번째 이후 element들이 주어졌다면 begin 인덱스부터 삽입된다
  3. .concat()
    신규 항목을 배열의 맨 뒤에 추가하고 리턴함
  4. .length
  5. Spread Operator : 깊은 복사
    1
    2
    3
    4
    5
    6
    7
    // 얕은 복사
    let shallowCopy1 = [1, 2, 3];
    let shallowCopy2 = shallowCopy2 // 혹은 shallowCopy1.slice();

    // 깊은 복사
    let deepCopy = [1, 2, 3];
    let deepCopy = [...deepCopy];
  • 배열 arr이 있고 weight가 주어졌을 때 합쳐서 weight가 되는 배열 내 항목 두 개의 인덱스를 찾기 (단, weight가 되는 두 값이 없을 경우 -1을 리턴)
    1
    2
    3
    4
    5
    6
    7
    8
    const findSum = (arr, weight) => {
      for (let i = 0, arrLength = arr.length; i < arrLength; i++) {
        for (let j = i+1; j < arrLength; j++) {
          if (arr[i]+arr[j] == wieght) return [i, j]
        }
      }
      return -1;
    } // n길이의 배열을 순회하는 for문이 두개 중첩되므로 시간 복잡도는 O(n의 2승)
  • 좀 더 알아보기
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    const findSumBetter = (arr, weight) => {
      let hashtable = {};
      for (let i = 0, arrLength = arr.length; i < arrLength; i++) {
        let currEl = arr[i], subVal = weight - currEl;
        if (hashtable[currEl] != undefined) return [i, hashtable[currEl]]
        else hashtable[subVal] = i;
      }
      return -1;
    } // 차이를 저장하고 해시테이블에 저장함으로써 O(n) 복잡도로 감소
    // 대신 공간 복잡도는 O(n) (해시테이블 만큼) 으로 늘어남
  • 두 개의 정렬된 배열이 동일한 크기일 때 해당 배열들의 중앙값 찾기
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    const medianOfArray = arr => {
      let len = arr.length;
      if (len % 2 === 1) return arr[Math.floor(length/2)]
      else return (arr[len/2] + arr[len/2-1])/2
    }

    const medianOfTwoSortedArr = (arr, arr2, pos) {
      // 배열의 길이가 0보다 같거나 작다면 -1을 리턴
      if (pos <= 0)
        return -1;
      // 배열의 길이가 1이라면 각 배열의 값을 더하고 2로 나눈 값을 리턴
      if (pos === 1) 
        return (arr[0] + arr2[0])/2
      // 배열의 길이가 2라면 0번째값의 최대값, 1번째값의 최소값을 구해 합하고 2로 나눈값을 리턴
      if (pos === 2) { 
        return (Math.max(arr[0], arr2[0]) + Math.min(arr[1], arr2[1]))/2;
      }
      // 두 배열의 중간값을 구하고
      let median = medianOfArr(arr);
      let median2 = medianOfarr(arr2);

      // 중간값이 같다면 어느 한쪽을 리턴
      if (median === median2) { 
        return median1;
      }

      // 짝수 길이의 배열이라면 offset값을 부여
      let evenOffset = pos % 2 === 0 ? 1 : 0
      // 배열 중간값을 앞뒤로 찾아보기 위해 인덱스 절반값에서 빼고 더한다
      let offsetMinus = Math.floor(pos/2) - evenOffset,
          offsetPlus = pos - Math.floor(pos/2) + evenOffset;
        
      // 첫번째 배열(arr)의 중간값이 두번째 배열(arr2)의 중간값보다 작다면
      // arr[arr[중간값], arr[중간값+1]], arr2[arr2[중간값-1], arr2[중간값]]를 매개변수로 재귀호출
      // 이 함수는 pos값이 2보다 작거나 같을 때 끝남 (분할 정복)
      if (median < median2) {
        return medianOfTwoSortedArray(arr.slice(offsetMinus), arr2.slice(0, -offsetMinus), offsetPlus);
      } else {
        return medianOfTwoSortedArray(arr2.slice(offsetMinus), arr1.slice(0, -offsetMinus), offsetPlus);
      }
    } // 매번 배열을 반으로 나누므로 시간 복잡도는 O(log2(n))이다
  • k개의 정렬된 배열에서 공통 항목 찾기
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    const commonElements = kArray => {
      let hashmap = {}, last, answer = [];
      for (let i = 0, kArrLen = kArray.length; i < kArrLen; i++) {
        let currArr = kArr[i];
        last = null;
        for (let j = 0, currArrLen = currArr.length; j < currArrLen; j++) {
          let currEl = currArr[j];
          // 배열값을 받아 hashmap에 접근하여 값이 없다면 1로, 있다면 ++한다
          if (last != currArr) {
            if (!hashmap[currEl]) 
              hashmap[currEl] = 1;
            else 
              hashmap[currEl]++
          }
          // 이 배열을 정렬된 배열이므로
          // 마지막으로 꺼내온 배열의 원소를 last로 저장하여 
          // 다음 인덱스에 같은 값이 나온다면 패스하도록 설정
          last = currEl
        } 
      }

      for (let prop in hashmap) {
        // 배열의 갯수만큼 있어야 공통값임
        if (hashmap[prop] === kArray.length) 
          answer.push(parseInt(prop)) // push는 O(1)임
      }
      return answer;
    } // 시간 복잡도는 O(kn)
  • 자바스크립트 함수형 배열 메소드
  1. map 함수는 배열을 순회하며 배열의 모든 항목에 함수를 적용하고 변화된 새 배열을 리턴함
  2. filter 함수는 전달받은 조건을 충족시키는 요소만 있는 새 배열을 리턴함
  3. reduce 함수는 모든 항목을 하나의 값으로 결합함
  • 자바스크립트에는 다차원 배열이 없는 대신 가변 배열이 있다
  • 배열의 나선형 출력
    → 왼쪽에서 오른쪽으로, 위에서 아래쪽으로, 오른쪽에서 왼쪽으로, 아래쪽에서 위로 출력하기
    → 네 가지 연산에 제한을 걸기
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    let M = [
      [1,2,3,4,5],
      [6,7,8,9,10],
      [11,12,13,14,15],
      [16,17,18,19,20]
    ]

    const spiralPrint = M => {
      let topRow = 0, leftCol = 0, btmRow = M.length-1, rightCol = M[0].length-1;
      while (topRow < btmRow && leftCol < rightCol) {
        for (let col = 0; col <= rightCol; col++) 
          console.log(M[topRow][col]);
      topRow++;
      for (let row = topRow; row <= btmRow; row++)
        console.log(M[row][rightCol]);
      rightCol--;
      if (topRow <= btmRow) {
        for (let col = rightCol; col >= 0; col--) 
          console.log(M[btmRow][col]);
        btmRow--;
      }
      if (leftCol <= rightCol) {
        for (let row = btmRow; row > topRow; row--)
          console.log(M[row][leftCol]);
        leftCol++
      }
    } // 시간 복잡도 O(mn) (배열 순회이므로 이차원 배열의 m*n 크기만큼)
  • 틱택토 게임
    → for문으로 세개의 행 모두를 확인하고 모든 열을 확인하고 대각선을 확인
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    const checkRow = (rowArr, letter) => {
      for (let i = 0; i < 3; i++){
        if (rowArr[i]!=letter) return false;
      }
      return true;
    } // 가로

    const checkCol = (boardMatrix, colIdx, letter) => {
      for (let i = 0; i < 3; i++) {
        if(boardMatrix[i][colIdx] != letter) return false;
      }
      return true;
    } // 세로

    const ticTackToe = (boardMatrix, letter) => {
      let rowWin = checkRow(boardMatrix[0], letter) 
          || checkRow(boardMatrix[1], letter) 
          || checkRow(boardMatrix[2], letter) 

      let colWin = checkCol(boardMatrix, colIdx[0], letter) 
          || checkCol(boardMatrix, colIdx[1], letter) 
          || checkCol(boardMatrix, colIdx[2], letter) 
      let digonalLeft = (
        boardMatrix[0][0] == letter 
        && boardMatrix[1][1] == letter 
        && boardMatrix[2][2] == letter
      )
      let digonalRight = (
        boardMatrix[2][0] == letter
        && boardMatrix[1][1] == letter
        && boardMatrix[0][2] == letter
      )
      return rowWin || colWin || digonalLeft || digonalRight;
    }
  • 길 찾기
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    const findChar = (char, matrix) => {
      let row = matrix.length, col = matrix[0].length;
      for (let i = 0; i < row; i++) {
        for (let j = 0; j < col; j++) {
          if (matrix[i][j] === char) return [i,j]
        }
      }
    }

    const pathRinder = matrix => {
      let row = matrix.length, col = matrix[0].length;
      let start = findChar('e', matrix), end = findChar('x', matrix);
      path (start[0], start[1]);

      function path(x,y) {
        if (x - row - 1 || y > col -1 || x < 0 || y < 0) return false
        if (x === end[0] && y === end[1]) return true;
        if (matrix[x][y] == '%' || matrix[x][y] == '+') return false
        matrix[x][y] = '+';

        if (path(x, y-1) || path(x+1, y) || path(x-1, y) || path(x-1, y)) return true;
        matrix[x][y] = '.';
        return false
      }
    }
  • 행렬 회전
    → 행렬의 세 번째 열이 회전된 행렬의 첫 번째 행이 된다
    → 행렬의 두 번째 열이 회전된 행렬의 두 번째 행이 된다
    → 행렬의 첫 번째 열이 회전된 행렬의 세 번째 행이 된다
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    const rotateMatrix = matrix => {
      let len = matrix.length;
      for (let x = 0; x < len; x++) {
        for (let y = x; y < len - x - 1; y++){
          // 현재값을 임시로 저장
          let temp = matrix[x][y];
          // 현재 값의 오른쪽 값을 위로 옮김
          matrix[x][y] = matrix[y][len-1-x];
          // 현재 값의 아래 값을 오른쪽으로 옮김
          matrix[y][len-1-x] = matrix[len-1-x][n-1-y];
          // 현재 값의 왼쪽 값을 밑으로 옮김
          matrix[len-1-x][len-1-y] = matrix[len-1-y][x];
          // 임시변수값을 왼쪽으로 옮김
          matrix[len-1-y][x] = temp;
        }
      }
    }

Comment and share

21-03-10 자바스크립트로 하는 자료구조와 알고리즘(2)

in 알고리즘, 서적

3장 자바스크립트 숫자

  • 자바스크립트에서는 숫자에 대해 64비트 부동소수점 표현을 사용한다
    → 부호 1비트 + 지수 11비트 + 소수 52비트
  • 십진분수로 인해 반올림 오류를 일으킬 수 있다 0.1 + 0.2 === 0.3; // false
  • Number 객체에 내장된 속성들
    1. 정수 반올림
      1
      2
      3
      Math.floor // 내림
      Math.round // 반올림
      Math.ceil // 올림
    2. Number.EPSILON : 두 개의 표현 가능한 숫자 사이의 가장 작은 간격을 리턴함
    3. 가장 큰 정수 : Number.MAX_SAFE_INTEGER
      Number.MAX_SAFE_INTEGER + 1 === Number.MAX_SAFE_INTEGER + 2 // true
    4. 가장 작은 정수 : Number.MIN_SAFE_INTEGER
      Number.MIN_SAFE_INTEGER - 1 === Number.MIN_SAFE_INTEGER - 2 // true
    5. 양의 무한(Infinity)값은 Number.MAX_SAFE_INTEGER보다 큰 유일한 값이며 음의 무한(-Infinity)값은 Number.MIN_SAFE_INTEGER보다 작은 유일한 값이다
  • 숫자 알고리즘
    1. 소수 테스트
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      function isPrime(n) {
        if (n <= 1) return false;

        for (let i = 2 i < n; i++){
          if (n%i == 0) {
            return false
          }
        }
        return true
      }
      // 시간 복잡도 O(n)
      1-1. 개선된 소수 테스트
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      // 소수는 6k±1의 형태를 지님
      // ex) 5 = 6-1, 7 = ((1*6) + 1), 13 = ((2*6) + 1) 등

      function isPrimeAdvanced(n) {
        if (n <= 1) return false
        if (n <= 3) return true

        if (n%2 == 0 || n%3 == 0) return false;

        for (let i = 5; i * i <= n; i=i+6){
          if (n%i == 0 || n % (i+2) == 0) return false;
        }
        return true;
      }
      // 시간 복잡도 O(sqrt(n))
    2. 소인수분해
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      function primeFactors(n) {
        while (n%2 == 0) {
          console.log(2);
          n = n/2
        }
        // n%2가 0이 아닐때까지 나눠 n은 이 시점에서 홀수가 됨
        for (let i = 3; i * i <= n; i = i+2){
          // i가 n을 나눌 수 있는 한 계속해서 i가 출력되고 n을 i로 나눈다
          while (n%i == 0) {
            n = n/i
          }

          if (n > 2) {
            console.log(n);
          }
        }
      }
      primeFactors(10) // 5, 2를 출력
      // 시간 복잡도 O(sqrt(n))
    3. 무작위 수 생성
      1
      Math.random() * n + x // x부터 (n+x)까지의 랜덤한 정수를 생성한다
    4. 모듈러 제곱거듭(modular exponentiation) : 단순한 계산법
      1
      2
      3
      const modularExponentiation = (x, y, p) => {
        return Math.pow(x, y) % p
      }
      4-1. 모듈러 제곱거듭(modular exponentiation) : 큰 지수도 다룰 수 있는 함수
      → 임의의 a와 b에 대해 c % m = [(a % m)(b % m)] % m이 성립
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      26
      27
      28
      29
      30
      31
      32
      33
      34
      const modularExponentiation = (base, exponent, modulus) => {
        if (modulus == 1) return 0;

        // 1. 값 = 1로 설정한다. 지수는 0이다
        let value = 1;

        // 2. 현재 지수를 1만큼 증가시킨다  
        for (let i = 0; i < exponent; i++) {
           // 3. 현재 지수가 목표의 지수가 될 때까지 
           // '값 = (값 x 기저) % 모듈러'를 반복한다
          value = (value * base) % modulus;
        }
        return value;
      } 
      ```  
      5. n보다 작은 소수 찾기
      ```javascript
      const allPrimesLessThanN = n => {
        for (let i = 0; i < n; i++){
          if (isPrime(i)) console.log(i);
        }
      }

      const isPrime = n => {
        if (n <= 1) return false
        if (n <= 3) return true

        if (n%2 == 0 || n%3 == 0) return false;

        for (let i = 5; i * i <= n; i=i+6){
          if (n%i == 0 || n % (i+2) == 0) return false;
        }
        return true;
      }
    5. 소인수 집합 확인
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      // 모든 소인수는 2와 3과 5로 나눠질 수 있다
      const maxDivide = (number, divisor) => {
        while (number % divisor === 0) number /= divisor;
        return number
      } // 시간 복잡도는 O(divisor를 밑으로 하는 log (number))

      const isPrimeFactor = number => {
        number = maxDivide(number, 2)
        number = maxDivide(number, 3)
        number = maxDivide(number, 5)
        return number === 1;
      } // 시간 복잡도는 O(log2(n))

      const primeFactorArr = n => {
        let count = 0, currNum = 1, primeNums = [];

        while (count != n) {
          if (isPrimeFactor(currNum)) {
            count++;
            primeNums.push(currNum)
          }
          currNum++
        }
        return primeNums;
      } // 시간 복잡도는 O(n(log2(n))) O(n번 * isPrimeFacor의 BigO 값)

      4장 자바스크립트 문자열

  • 자바스크립트의 기본 자료형인 String에는 다양한 함수가 존재
  1. 문자에 접근할 때엔 .charAt()을 사용한다 'dog'.charAt(1) // "o"
    1-1. substring(startIdx, endIdx)을 사용하면 지정된 값 사이의 문자열의 리턴이 가능하다
    1-2. 이때 endIdx를 입력하지 않는다면 자동으로 문자열 마지막까지 리턴한다
  2. 문자열을 비교할 때에는 < 나 > 기호를 통해 쉽게 비교할 수 있다
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    let a = 'a'
    let b = 'b'
    console.log(a < b) // true
    /*------------------------------*/
    // 길이가 다른 문자열을 비교한다면 문자열의 시작부터 비교하여
    // 더 짧은 길이의 문자열길이만큼만 비교한다
    a = 'add'
    b = 'b'
    console.log(a < b) // true
    /*------------------------------*/
    a = 'add'
    b = 'ab'
    console.log(a < b) // false
  3. 문자열 내 특정 문자열을 찾기 위해 .indexOf(searchValue[, fromIndex])를 사용할 수 있다
    3-1. 검색하고자하는 문자열을 매개변수로 받으며 선택적으로 검색 시작의 인덱스를 받을 수 있다
    3-2. 이 함수는 일치하는 문자열의 위치를 리턴하며 대소문자를 구분한다
    3-3. 없다면 -1을 리턴하므로 -1을 반환하는지 아닌지를 확인하면 된다
  4. 문자열을 분해할 때에는 .split(separator)를 사용할 수 있으며 분리자 매개변수를 받아 부분 문자열 배열을 생성한다
  5. .replace(string, replaceString)함수는 문자열 내 특정 문자열을 대체하는 함수이다
  6. 정규 표현식은 검색 패턴을 정의한 문자열의 집합으로 기본 객체 RegExp를 사용할 수 있다
    6-1. RegExp의 생성자는 정규 표현식과 일치 관련 설정의 두 가지 매개변수를 받는다
    6-2. i는 대소문자를 구분하지 않고 일치하는 문자열을 검색하며, g는 전역적으로 ((모든) 문자열을 검색하며, m은 다중열 문자열에 대해서도 일치하는 문자열을 검색한다
    6-3. RegExp는 search()와 match() 함수가 존재하며 search()는 찾은 문자열의 인덱스를, match()는 모든 일치하는 문자열을 리턴한다
    6-4. String 객체에서 RegExp를 매개변수로 받는 함수는 일치하는 문자열을 찾는 exec()와 문자열을 찾아 boolean값을 리턴하는 test()가 있다
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    <--- 기본 정규 표현식 --->
    ^ :문자열/줄의 시작을 나타냄
    \d : 모든 숫자를 찾는다
    [abc]/[^abc] : 괄호 내 모든 문자를 찾는다 / 제외한 문자열을 찾는다
    [0-9]/[^0-9] : 괄호 내 모든 숫자를 찾는다 / 제외한 숫자를 찾는다
    (x|y) : x나 y 문자열을 찾는다
    <--- 자주 사용되는 정규 표현식 --->
    /\d+/ : 숫자를 포함하는 문자
    /^\d+$/ : 숫자만 포함하는 문자
    /^[0-9]*.[0-9]*[1-9]+$/ : 부동 소수점 문자
    /[a-zA-Z0-9]/ : 숫자와 알파벳만 포함하는 문자
    /([^?=&])(=([^&]*))/ : 질의 문자열
  7. 자바스크립트의 base() 함수는 문자열로부터 Base64 인코딩된 ASCII 문자열을 생성하며 atob() 함수는 Base64 인코딩된 문자열을 디코딩하는 함수이다
    7-1. 단축 URL은 이 base() 함수를 응용하여 사용하는 것이다
  8. RSA 암호화는 키 생성, 암호화, 복호화의 3단계가 있으며 매우 큰 소수를 사용하여 소인수분해(4096비트 소수 곱을 사용)의 역계산을 어렵게 한다

Comment and share

21-03-08 자바스크립트로 하는 자료구조와 알고리즘(1)

in 알고리즘, 서적

1장 빅오 표기법

O(1)은 신성하다 - 하미드 티주쉬

  • 빅오 표기법 기초

    • 빅오 표기법에서 n은 입력의 개수를 나타낸다
    • “n이 무한으로 접근할 때 무슨 일이 일어날까?”
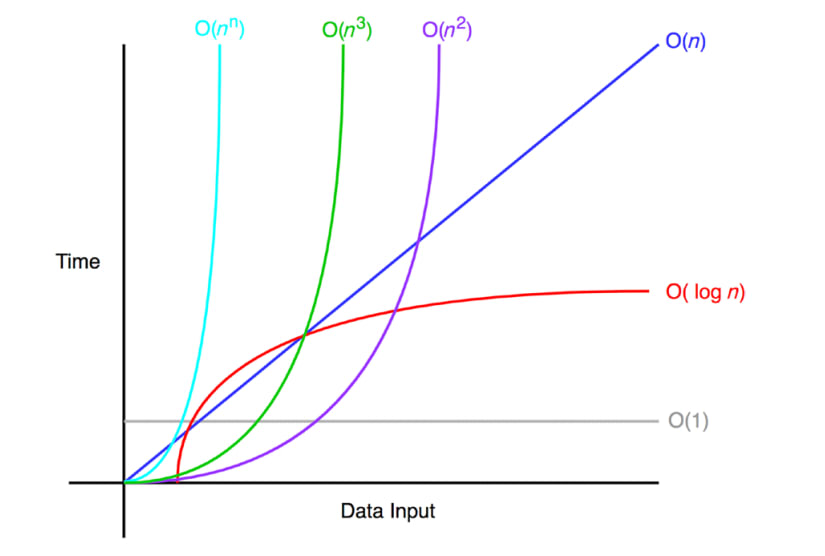
      일반적인 빅오 복잡도 그래프

  • 계수 법칙 : “상수를 제거하라”

  • *

    상수 k > 0인 경우 f(n)이 O(g(n)이면 kf(n)은 O(g(n))이다
    **

    1
    2
    3
    4
    5
    6
    function Coefficient(n) {
      let count = 0;
      for (let i = 0; i < n; i++) count += 1
      return count;
    }
    // Coefficient(n)의 복잡도는 O(n)

  • 합의 법칙 : “빅오를 더하라”

  • *

    f(n)이 O(h(n))이고 g(n)이 O(p(n))이라면 f(n)+g(n)은 O(h(n)+p(n))이다
    **

    1
    2
    3
    4
    5
    6
    7
    function SumBigO(n) {
      let count = 0;
      for (let i = 0; i < n; i++) count += 1;
      for (let i = 0; i < 5*n; i++) count += 1;
      return count;
    }
    // SumBigO(n)의 복잡도는 O(n + 5n) = O(n)이 된다

  • 곱의 법칙 : “빅오를 곱하라”

  • *

    f(n)이 O(h(n))이고 g(n)이 O(p(n))이라면 f(n)g(n)은 O(h(n)p(n))이다
    **

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    function MultipleBigO(n) {
      let count = 0;
      for (let i = 0; i < n; i++) { 
        count += 1;
        for (let i = 0; i < 5*n; i++) 
          count += 1;
      }
      return count;
    }
    // MultipleBigO(n)의 복잡도는 O(n^2)

  • 다항 법칙 : “빅오의 k승”

  • *

    f(n)이 k차 다항식이라면 f(n)은 O(n^k)이다
    **

    1
    2
    3
    4
    5
    6
    7
    8
    9
    function PolynomialBigO(n) {
      let count = 0;
      for (let i = 0; i < n*n; i++) { 
        count += 1;

      }
      return count;
    }
    // PolynomialBigO(n)의 복잡도는 O(n^2)

    2장 자바스크립트의 독특한 특징

  • 자바스크립트는 동적 인터프리터 프로그래밍 언어이기 때문에 다른 객체지향 프로그래밍 언어들과는 구문이 다름

  • 자바스크립트의 범위(scope)

    • 전역 선언: 전역 범위
      → 전역 선언은 안좋은 방법이므로 되도록 사용하지 말 것
    • var를 사용해 선언 : 함수 범위
      → var를 사용하면 변수를 어디에 선언하더라도 함수의 맨 앞으로 이동한다
      → 이를 변수 호이스팅(variable hoisting)이라고도 한다
      1
      2
      3
      4
      5
      6
      7
      8
      9
      function scope1() {
        var top = "top"
        bottom = "bottom";
        console.log(bottom)

        var bottom;
      } 
      // bottom은 맨 마지막에 선언되었지만 
      // console.log() 앞으로 hoisting되며 오류 없이 실행된다
    • var로 선언된 해당 변수의 범위가 가장 가까운 함수 범위가 된다
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      function scope2(print) {
        if (print) {
          var insideIf = '12';
        }
        console.log(insideIf);
      }
      scope2(true);

      function scope2_copy(print) {
        var insideIf;
        if (print) {
          insideIf = '12';
        }
        console.log(insideIf);
      }
      scope2_copy(true);
      // scope2와 scope2_copy는 동일하게 실행된다
    • let를 사용해 선언 : 블록 범위
      → 변수가 선언된 블록 범위({})내에서 유효하다
      1
      2
      3
      4
      5
      6
      7
      8
      9
      function scope3(print) {
        if(print) {
          let insideIf = '12'
        }
        console.log(insideIf);
      }
      scope3(true);
      // 오류가 발생함 let은 블록 범위에서만 유효하기 때문에
      // if문을 벗어나면 해당 변수를 읽을 수 없다

  • 등가와 형

    • 자바스크립트에는 boolean, number, string, undefined, object, function, symbol과 같은 일곱가지의 기본 자료형이 존재함
    • 값이 선언만 되고 값이 할당되지 않으면 undefined가 됨
    • 타 언어에서 대개 if문 내 매개변수는 boolean형이어야 하지만 자바스크립트에서는 해당 변수가 비었거나 null이거나 undefined라면 false로 평가된다
    • false로 인식되는 값은 false 외에 0, ‘’(혹은 “”), NaN, undefined, null가 있고 0이 아닌 숫자, 비어있지 않은 문자열이나 객체를 true로 평가한다
    • 자바스크립트는 스크립트 언어이기 때문에 코드가 실행될 때 해당 변수의 형이 해석된다
    • ==는 값만 확인하지만 ===는 형과 값을 모두 확인 한다
      "5" == 5 // true vs "5" === 5 // false
    • 자바스크립트에서 동일한 속성과 값을 갖는 두 객체가 동일한지 확인하고자 ==를 사용한다면 변수의 메모리 주소가 다르기 때문에 false를 리턴할 것이다
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      function isEquivalent(a,b) {
        var aProps = Object.getOwnPropertyNames(a);
        var bProps = Object.getOwnPropertyNames(b);

        // 길이가 다르다면 두 객체는 다른 객체임
        if (aProps.length != bProps.length) return false
        for (var i = 0; i < aProps.length; i++) {
          var propName = aProps[i];

            // 속성값이 다른 경우 두 객체는 같지 않다
            if(a[propName] !== b[propName]) return false
        }

        return true;
      }
      isEquivalent({'hi':12},{'hi':12}); // true

Comment and share

21-03-08 알고리즘 강의 노트정리(2)

in 알고리즘

소 저녁 식사 주기

  • N(1~15)마리의 소들을 순서대로 세워놓고 각 소들 사이에 +, -, .의 셋 중 한가지가 쓰여진 냅킨을 배치해서 최종 결과가 0이 되도록 하는 문제
  • .은 숫자를 연결하는 부호가 됨 (예: 10.11 => 1011)
  • 소의 수 N이 입력되었을 때 처음 20줄에 대해 가능한 20가지 답을 출력하는데 사전 순으로 앞선 것을 출력한다
  • +가 가장 앞서고 -, . 순서이다

N = 7
1 + 2 - 3 + 4 - 5 - 6 + 7
1 + 2 + 3 + 4 - 5 + 6 - 7
1 - 2 + 3 + 4 - 5 + 6 - 7
1 - 2 - 3 - 4 - 5 + 6 + 7
1 - 2 . 3 + 4 + 5 + 6 + 7
1 - 2 . 3 - 4 . 5 + 6 . 7
6 가지

  • 수와 수 사이에 사용할 수 있는 연산자는 모두 3종류
  • 수와 수 사이의 개수는 N-1개이므로 가능한 경우의 수는 3의 N-1승 가지 이다
  • N의 최대값이 15이므로 3의 14승 = 4,782,969 가지가 최대치가 됨
  • 두 수 사이에 +나 -를 사용하는 경우에는 dfs(step, a)로 해결
  • 하지만 .을 고려한다면 dfs(step, a, b)로 구현해야 함
  • 여기서 a는 직전에 등장한 + 또는 - 이전까지의 결과이고 b는 직전에 등장한 + 또는 - 이후부터 0개 이상의 .을 계산하여 하나의 수로 만든 결과
  • 새로운 +나 -가 나오면 a에 b에 더하는 연산만 한다 (-일 때엔 b를 음수로 변환)
  • 마지막 단계에서 a + b === 0 인지를 확인
  • N의 최대값이 15이므로 만들 수 있는 가장 큰 수는 123456789101112131415이지만 결과값이 0이어야 하므로 12345678910 이상의 수는 고려하지 않아도 된다 (나머지인 1112131415가 12345678910보다 작기 때문)

Comment and share

21-03-08 알고리즘 강의 노트정리

in 알고리즘

단어 세기

  • 해당 강의에서는 C++의 string.h 라이브러리 내 strtok() 함수를 사용하여 해결하였으나 자바스크립트에서는 널 포인트를 사용하지 않기 때문에 따로 구현하고 넘어감
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
const countWords = p => {
    let divide = p.split('\n').map(el => el.split(' '))
    for(let i = 0; i < divide.length; i++) {
        let result = [];
        for (let j = 0; j < divide[i].length; j++){
            let fCondition = divide[i][j];
            // 객체 내의 원소를 받고 해당 원소로 배열을 필터
            // 필터된 배열의 길이가 해당 아이템의 숫자가 됨
            let cnt = divide[i].filter(el => el === fCondition).length;
            let element = `${fCondition} : ${cnt}`
            if(!result.includes(element))
                result.push(element)
        }
        result = result.sort((a,b) => a.charCodeAt() - b.charCodeAt())
        console.log(result);
    }
}
  • 출력 예제와 다른 점 : sort()함수를 사용하여 ASCII 값을 비교하여 정렬하였으나 출력 예제의 ‘A : 1’, ‘AM : 2’, ‘DOG : 4’, ‘I : 2’와는 달리 ‘AM : 2’, ‘A : 1’, ‘DOG : 4’, ‘I : 2’로 출력되었다
  • 어떻게 해결하면 될까?를 고민해봐야 함

Comment and share

21-03-07 알고리즘 강의 노트정리

in 알고리즘

진법을 변환하기

  • A진법 수 N을 입력 받아 B진법 수로 변환하는 문제
  • Horner’s Method

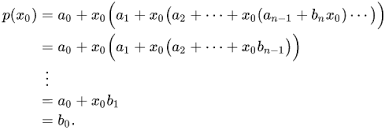
    → 해시 문제나 긴자리수 진법 변환 문제에 사용됨
  • 2진수를 10진수로 변환하기
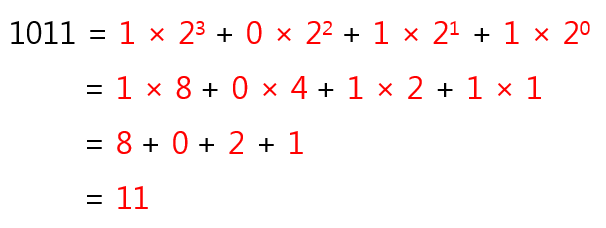
  • 예1) 2진법 11010을 8진법으로 바꾸어보자
    → char str[] = “11010”
    (의미는 없지만 JS에서는 let str = Number(10110).toString()로 표현가능함)

d = d * 2 + ‘1’ - ‘0’; // d(3) = 1 * 2 + 1
d = 02 + 1 = 1
d = 12 + 1 = 3
d = 32 + 0 = 13
d = 62 + 1 = 13
d = 13*2 + 1 = 26

  • 10진법을 먼저 구하고 10진법 26을 8진법으로 바꾸기

    38 + 2 ``26/88 + 26%8(0*8 +**3**) * 8 + **2**(3/88 + 3%8)*8 + 26%8``
    *    32** (Octet)

  • 예2) 10진법 2543을 16진법으로 바꾸기

    158 * 16 + ‘F’ 2543/16 * 16 + 2543%16 // 158*16 + 15
    (916 + ‘E’) * 16 + ‘F’ ``(158/16)*16 + 158%16 + ‘F’ // 916 + 14 + ‘F’``
    ((016 + 9) * 16 + *‘E’*) * 16 + *‘F’** = 9EF (Hexadecimal)

자바스크립트의 진법 변환은 매우 간단하기 때문에 별도의 코드는 첨부하지 않음

1
2
3
4
let value = 10;
value.toString(2) // 2진법으로 변경
let binary = 1010;
Number.parseInt(binary, 2) // 10진법으로 변경

앞뒤 같은 제곱

  • N(1≤N≤300)중에서 N의 제곱값을 B(2≤B≤20)진수로 바꿨을 때 앞뒤가 같은 수가 되는 N값과 N의 제곱값을 B진수로 바꾸는 문제 (단, 10보다 큰 숫자는 A~J로 표현)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
const changeNumBase = powNum => {
    let arr = [];
    for (let i = 1; i <= 300; i++) {
        arr.push(Math.pow(i, powNum))
    }
    arr = arr.filter(num => {
        return num.toString() === num.toString().split('').reverse().join('');
    })

   return arr;
}

const solution = () => {
    let arr = [];
    for (let i = 2; i <= 20; i++) {
        arr.push(changeNumBase(i));
    }
    return arr.filter(el => el.length > 1)
}

/* 출력 예시
[
  [     1,     4,     9,
      121,   484,   676,
    10201, 12321, 14641,
    40804, 44944, 69696
  ],
  [ 1, 8, 343, 1331, 1030301, 1367631 ],
  [ 1, 14641, 104060401 ]
]
*/

Comment and share

21-03-06 알고리즘 강의 노트정리

in 알고리즘

연속부분합 찾기

  • sliding window 방식을 이용한 연속부분합
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    const slidingWindow = (arr) => {
        let N = arr.length;
        let answer = Number.MIN_SAFE_INTEGER;
        /* 부분합을 구할 배열의 길이를 늘려가며 해답을 찾기
         최소값은 1이고 최대값은 배열의 길이만큼 */
        for (let len = 1; len <= N; len++) {
            let sum = 0
            /* scanf로 값을 불러오는 C++ 코드와는 달리 
            배열을 받아 처리하는 함수로 작성하였기 때문에 
            i = 0부터 시작해서 i+1값이 length값보다 커지면 
            앞부분을 잘라내도록 변경 */
            for (let i = 0; i < N; i++) {
                // i값이 len 보다 길어지면 현재 벗어난 i-len 인덱스 부분의 값을 빼줌
                if (i+1 > len) sum -= arr[i-len]
                // 슬라이딩하여 추가된 값을 더해줌
                sum += arr[i]
                /* i+1 >= len, 즉, 해당 부분 배열의 길이가 같고
                   부분합이 기존의 answer보다 크다면 갱신 */
                if (i+1 >= len && answer < sum) answer = sum;
            }
        }
        return answer
    }
  • prefix sum 방식으로 찾기
    → prefix를 사용하기 위해서는 0번째 원소(누산용 초기값 0)가 필요하다
    → 처음에 배열을 그대로 썼을 때 arr의 N번째값이 없어서 preSum의 마지막 값으로 NaN값이 출력됨
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    const prefixSum = arr => {
        let answer = Number.MIN_SAFE_INTEGER;
        arr = [0, ...arr];
        let preSum = Array.from({length: arr.length + 1}, () => 0)
        // prefix를 사용하기 위해서는 0번째 원소(누산용 초기값 0)가 필요하다
        for (let i = 1; i <= N; ++i) {
            preSum[i] = preSum[i-1] + arr[i]
        }
        // 처음에 배열을 그대로 썼을 때 arr의 N번째값이 없어서 preSum의 마지막 값으로 NaN값이 출력됨
        for (let length = 1; length <= N; length++) {
            for (let i = length; i <= N; i++) {
                if (preSum[i] - preSum[i-length] > answer)
                    answer = preSum[i] - preSum[i - length]
            }
        }
        return answer;
    }
  • dynamic programming 방식으로 찾기
    • D[i]를 i번째 수를 마지막으로 하는 연속 부분합의 최대값으로 정의
    • 연속 부분합이므로 A[i]를 새로운 부분합의 시작으로 하지 않는 한 D[i]값은 D[i-1]을 이용할 수 밖에 없다
    • D[i-1] <= 0이라면 D[i-1]값을 고려할 필요가 없다
    • D[i] = max(A[i], D[i-1] + A[i])
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      const dynamicSum = arr => {
          let answer = Number.MIN_SAFE_INTEGER;
          let N = arr.length
          arr = [0, ...arr] // 마찬가지로 0번째에 누산용 0값을 입력
          D = Array.from({length: N}, () => 0)
          for (let i = 1; i <= N; i++) {
              // D[i-1] 값이 음수라면 더해도 최대값이 될 수 없다
              D[i - 1] > 0 ? D[i] = D[i - 1] + arr[i] : D[i] = arr[i]
          
              if (D[i] > answer) answer = D[i]
          }
          return answer
      }
  • 메모이제이션으로 배열을 사용하지 않고 해결하기(Kadane’s Algorithm)
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    const dynamicSum = arr => {
        let answer = Number.MIN_SAFE_INTEGER;
        let N = arr.length
        arr = [0, ...arr]
        let sum = 0;
        for (let i = 1; i <= N; i++) {
            // D[i-1] 값이 음수라면 더해도 최대값이 될 수 없다
            sum > 0 ? sum += arr[i] : sum = arr[i]
            if (sum > answer) answer = sum
        }
        return answer
    }
  • 배우면서 느꼈던 것
    → 상황에 따라 배열의 인덱스 값을 고려하여 코딩해야 한다는 점을 기억하자
    → 0을 맨 앞에 추가했다면 1번째 원소부터 고려해야 한다

회전 초밥 문제

  • 손님이 k개의 접시를 연속해서 먹을 경우 할인된 가격으로 제공
  • 위 행사에 참여하면 초밥을 선택할 수 있는 쿠폰을 발행
  • 회전 초밥 음식점의 벨트 상태 N, 메뉴에 있는 초밥의 가짓수 d, 연속해서 먹는 접시의 개수 k, 쿠폰 번호 c 가 주어짐
  • 이 때, 손님이 먹을 수 있는 최대 가짓수를 구하는 문제
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// 접시의 수(N), 초밥 가짓수(d), 연속해서 먹는 접시 수(k), 쿠폰번호(c)
// 초밥이 순서대로 담긴 배열(list)
const sushi = (N, d, k, c, list) => {
    let chk = Array.from({length: d+1}, () => 0)
    chk[c]++; // 쿠폰으로 먹을 수 있는 초밥을 미리 있다고 가정
    let cnt = 1;

    // 첫 k개의 접시는 먹은 것으로 간주하고 시작함
    for (let i = 0; i < k; i++) 
        if (chk[list[i]]++ === 0)
            cnt++
    
    let answer = cnt;

    for (let i = k; i < N + k; i++) {
        // list의 i-k 번째의 값에 -1 했을 때 0이라면 이미 먹은 접시이므로 빼준다
        if(--chk[list[i - k]] === 0) cnt--;
        // 회전하는 list이기 때문에 초과하는 값은 다시 돌아와야 하므로 i를 N으로 나눠준 나머지값으로 계산
        // chk 배열 내 list[i%N] 번째 값이 0이라면 +1로 더해주고 카운트 값도 +1함
        if(chk[list[i%N]]++ === 0) cnt++
        // 이 때 카운트 값이 현재의 최대값보다 크다면 갱신한다
        if(cnt > answer) answer = cnt;
    }
    return answer;
}

Comment and share

21-03-05 알고리즘 강의 노트정리

in 알고리즘

이진검색

  • 정렬된 리스트에서 특정한 값의 위치를 찾는 알고리즘
  • 전화번호부 반으로 찢어 찾기 (from CS50)
  • True/False 결과로 최적해를 탐색하는 방법
  1. 탐색 배열의 가운데 인덱스를 구함
  2. 만약 가운데 값이 해당 값과 같다면 찾은 것
  3. 주어지는 배열은 정렬되어 있으므로 가운데 값이 해당 값보다 작다면 우측 반을 검색범위로 지정 (mid+1, high)
  4. 반대의 경우라면 (low, mid+1)로 검색범위를 지정
  5. 위 과정을 반복하여 값을 찾음 (단, low > high가 된다면 해당 값이 배열에 없는 경우)

while문을 사용한 이진검색

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
const binarySearch = (
    arr = arr.sort((a,b) => a - b), low = 0, high = arr.length, target
    ) => {
        while(low <= high) {
            // 가운데 인덱스 구하기
            let mid = Math.floor((low + high)/2);

            // 가운데 값이 해당값과 같다면 찾은 것
            if (arr[mid] === target) return mid;

            // 해당 값보다 작다면
            if (arr[mid] < target) low = mid + 1

            // 해당 값보다 크다면
            if (arr[mid] > target) high = mid - 1
        }
    // 반복하는 동안 low > high가 된다면 해당 값이 배열에 없으므로 -1을 리턴
    return -1
}

재귀를 사용한 이진검색

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
const binarySearchRecursive = (
    arr = arr.sort((a,b) => a - b), low = 0, high = arr.length, target
) => {
    // 찾지 못한 경우
    if (low > high) return -1

    // mid값 구하기
    let mid = Math.floor((low + high)/2);

    // 가운데 값이 해당 값이라면 return
    if (arr[mid] === target) return mid 
    
    // 해당 값 보다 작거나 크다면 함수를 재귀 호출
    if (arr[mid] < target) return binarySearchRecursive(arr, mid+1, high, target)
    return binarySearchRecursive(arr, low, mid-1, target)
}

True/False 결과로 최적해를 탐색하는 방법

  • 구슬의 개수 N과 그룹의 수 M이 주어질 때 임의의 그룹 내 요소들의 최대값이 최소가 되게 하는 문제 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    const check = mid => {
        let group = 1, sum = 0;
        for (let i = 0; i < N; ++i) {
            // 첫번째 구슬부터 더하여 mid값보다 커지면 그룹화하고 새 그룹으로 넘어감
            if (sum + arr[i] > mid) {
                // mid가 10이라 가정하고 1, 2번째 값의 합이 8이 되고 
                // arr[2]값이 4라면 sum + arr[2] = 12가 되어 8보다 커지므로
                // sum값을 arr[2]값으로 초기화하고 그룹 수를 늘린다
                sum = arr[i];
                group++;
            } else {
                // 만약 합이 최대값을 넘기지 않는다면 더해주어도 괜찮음
                sum += arr[i]
            }
        }
        return group <= M
    }

    let low = 0, high = 0;
    let N = 8, M = 3
    let arr = [5, 4, 2, 6, 9, 3, 8, 7]
    const input = () => {
        console.log(`${N}개의 구슬을 ${M}개의 그룹으로 나누어야 합니다`)
        for (let i = 0; i < N; ++i){
            // console.log(arr[i])
            // 각 구슬 중에 최소값을 구함
            if (low < arr[i]) low = arr[i];
            // 구슬의 총합을 최대값으로 구함
            high += arr[i]; 
        }
    }

    const output = () => {
        console.log(answer);
        let count = 0, sum = 0, limit = M; // limit: 그룹 수 제한
        for (let i = 0; i <= N; ++i) {
            // 구한 해답이 arr[i]번째까지의 합보다 크거나 
            // 한 그룹당 하나 이상의 구슬이 있어야 하므로 N - M < i 보다 작아야 한다
            if (sum + arr[i] > answer || N - i < limit) {
                console.log(`그룹${i+1}:${count}`) // 그룹 수를 출력
                count = sum = 0; // 초기화
                limit--; // 남은 그룹 수 줄이기 
            } 
            sum += arr[i];
            count++;
        }
    }

    const process = () => {
        while (low <= high) {
            let mid = Math.floor((low + high) / 2);
            if (check(mid)) {
                answer = mid;
                high = mid - 1;
            } 
            // group <= M 가 false를 리턴 할 때 (그룹 수가 M을 넘어갈 때)
            else low = mid + 1
        }
    }

    const solution = () => {
        input();
        process();
        output();
    }

    solution();
  • 배우면서 이해가기 어려웠던 점
    • mid값은 index값이 아닌가? 왜 mid를 최대값으로 설정하여 check를 할까?
      → mid값은 최소값 + 최대값의 중간값
      → check 함수는 group <= M의 boolean 값을 리턴하므로 이 함수가 True값을 리턴할 때만 구슬의 합을 계산하면 된다

책 복사하기

  • 주어진 대본들의 페이지(m[])를 k명의 서기공이 한 파트 이상 복사할 때 가장 많은 페이지를 맡은 서기공의 페이지를 구하는 문제
  • 답이 두 개 이상 있다면 첫 번째 서기공이 할 일이 가장 작아야 하며 두 번째 서기공이 할 일이 작아야 한다
  • 입력값이 100,000으로 커서 순차 탐색보다 이진 탐색을 사용해야 한다
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    let arr = [100, 200, 300, 400, 500, 600, 700, 800, 900];
    let M = arr.length, K = 3;
    let low = 0, high = 0;

    const input = () => {
        console.log(`${M}개로 나누어진 대본을 ${K}명의 서기공이 나누어 일을 해야 합니다`); 
        for (let i = 0; i < M; ++i) {
            // 숫자 구슬과 유사함
            if (low < arr[i]) low = arr[i];
            high += arr[i]; 
        }
    }

    const check = mid => {
        let group = 1, sum = 0;
        for (let i = 0; i < M; ++i) {
            if (sum + arr[i] > mid) {
                sum = arr[i];
                group++;
            } else sum += arr[i];
        }
        return group <= K
    }

    const process = () => {
        while (low <= high) {
            let mid = Math.floor((low + high)/2);
            if (check(mid)) {
                answer = mid;
                high = mid - 1
            } else low = mid + 1
        }
    }

    const output = (index, sum, people) => {
        if (index < 0) return;
        if (sum + arr[index] > low || index < people) {
            output(index - 1, arr[index], people - 1);
            console.log(`${arr[index]} / `)
        } else {
            output(index -1, sum + arr[index], people);
            console.log(`${arr[index]} `)
        }
    }

    const solution = () => {
        input();
        process();
        output(M - 1, 0, K - 1);
        // 배열의 마지막 번째(M-1)값부터 탐색해 들어가면 재귀를 통해 첫번째 index부터 실행된다
        // 사람이 K명일때는 "/"가 K-1개 들어가야 하므로 K-1번만 수행한다
    }

    solution();
  • 숫자 구슬 문제를 이해하고 나면 생각보다 이해하기 쉬웠음
  • 재귀적으로 호출될 때 마지막부터 탐색한다면 LIFO 콜스택에 의해 가장 먼저 출력되는 것은 0번째 index일 것이다 (탈출구문은 0보다 작을 때로 작성)

Comment and share

Harry Kim

author.bio


author.job