탐욕법과 최소비용신장트리

• 동전 거스름돈 문제 슈도코드로 해결해보기

  1 2 3 4 5 6 7 8

  while (동전이 남아있고 문제가 미해결): 가장 가치가 높은 동전을 선택 if (동전을 더하여 거스름돈의 총액이 거슬러주어야 할 액수를 초과): 동전을 다시 집어넣는다 else: 거스름돈에 동전을 포함시킨다 if (거스름돈의 총액이 거슬러주어야 할 액수와 같다) 문제 해결 return

  이는 동전의 구성이 [500, 100, 50, 10, 5, 1]일때는 가능하지만 [500, 100, 80, 10, 5, 1]일 때엔 불가능함

• 탐욕법의 설계전략: 공집합에서 시작
  → 집합에 추가할 다음 최적의 원소를 고른다 (선택 과정)
  → 새로운 집합이 해답으로 적절한지 검사한다 (적절성 검사)
  → 새로운 집합이 문제의 해답인지 판단한다 (해답 점검)
  → 탐욕법은 상대적으로 설계하기 쉽지만 반드시 정확성을 증명해야 함

• 최소비용 신장트리 (MST:Minimum Spanning Tree) 문제
  → G = (V, E) : 모든 정점이 연결된 가중치가 있는 무방향 그래프
  → G의 부분 그래프 T = (V, F), F ⊆ E
  → 그래프 G의 모든 정점을 연결하는 트리, 간선의 개수는 n-1개
  → 이 때, 모든 신장트리 T 중에 가중치의 합이 최소가 되는 신장트리를 최소비용 신장트리라 함

• 최소비용 신장트리를 Brute-Force 방식으로 풀기
  → 모든 신장트리를 찾고 가중치의 합이 가장 작은 것을 선택
  → 간선의 개수가 n-1인 연결된 트리가 될때까지 간선을 제거

• 최소비용 신장트리를 Greedy 방식으로 풀기

1. 해답의 집합을 공집합으로 둔다: 간선 집합 E의 부분 집합 F를 공집합으로 둔다
2. E에서 최적의 간선 하나를 추출하여 F에 포함시킴
   → 최적을 선택할 때 사용되는 알고리즘에는 프림, 크루스칼 알고리즘이 있다

• 프림 알고리즘

1. Y = {V1}: Y는 정점의 집합 V의 부분 집합
2. Y에 최적의 원소 하나를 포함시킨다 (가중치가 가장 작은 정점 vnear를 선택)
   → F집합에 (nearest(vnear), vnear)를 추가
3. 해답의 집합이 최종이면 종료하고 아니면 2단계를 반복함
   → Y = V가 되면(모든 원소를 포함한다면) 종료

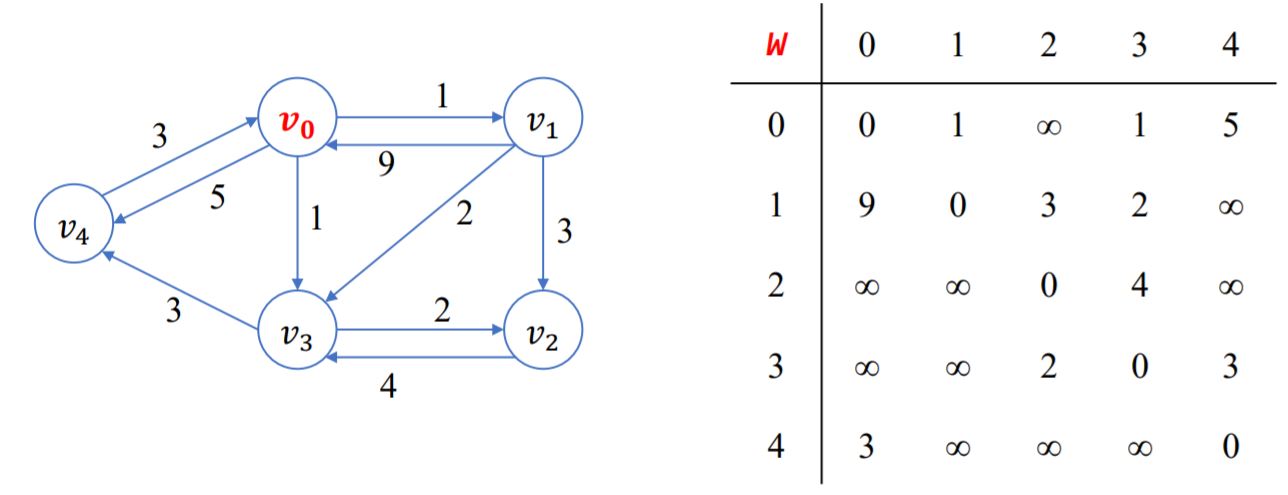
• 프림 알고리즘 어떻게 구현할까?
  → W[i][j]: 인접행렬 (간선의 가중치)
  → nearest[i] : Y 집합에서 vi에 가장 가까운 정점의 인덱스
  → distance[i] : vi와 nearest[i]의 정점을 연결하는 간선의 가중치

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

def prim (W):
    n = len(W) - 1
    F = []
    nearest = [-1] * (n + 1)
    distance = [-1] * (n + 1)
    for i in range(2, n+1):
        nearest[i] = 1
        distance[i] = W[1][i]
    for _ in range (n - 1):
        minValue = INF
        for i in range(2, n+1):
            if (0 <= distance[i] and distance[i] < minValue):
                minValue = distance[i]
                vnear = i
        edge = (nearest[vnear], vnear, W[nearest[vnear]][vnear])
        F.append(edge)
        distance[vnear] = -1
        for i in range(2, n+1):
            if (distance[i] > W[i][vnear]):
                distance[i] = W[i][vnear]
                nearest[i] = vnear
    return F

def cost (F):
    total = 0
    for e in F:
        total += e[2]
    return total

Comment and share

최적 이진검색트리

• 주어진 n개의 키로 최적 이진검색트리를 구하는 문제
  → 주어진 n개의 키: K1, K2…, Kn
  → 각 키의 검색 확률 pi: 전체 검색횟수 중에서 Ki를 검색하는 확률
  → 각 키의 비교 횟수 ci: Ki를 검색하는데 필요한 키의 비교 횟수
  → 각 키의 평균 검색 시간: 검색 확률 * 비교 횟수 (pi * ci)
  → 전체 키의 평균 검색 시간: pi * ci의 총 합(n ~ i=1)

• Dynamic Programming 방식으로 접근하기

  1. 재귀 관계식을 찾는다
  • A: 이진검색트리를 만드는데 최적 검색비용의 행렬
  • A[i][j]: Ki에서 Kj까지 이진검색트리를 만드는데 최적 검색 비용
  • Ki … Kj를 (Ki … Kk-1)Kk(Kk+1 … Kj)로 분할하는 재귀 관계식 찾기
  2. 상향식 방법으로 해답을 구하기
  • A[i][i] = pi
  • 대각선의 상향식 계산으로 A[1][n]을 구함
  3. 최적 이진검색트리의 재귀관계식
  • 트리 k: 키 Kk가 루트 노드에 있는 최적 이진검색트리
  • 키 비교 횟수: 서브 트리의 비교 횟수에 루트에서 비교 한 번 추가
  • m ≠ k 인 Km에 대해서 트리 k에 Km을 놓기 위한 비교 한 번 추가
    → A[1][n] = minimum(A[1][k-1]+A[k+1][n] + ∑(n ∼ m=1)Pm) (단, i ≤ k ≤ j)

파이썬으로 최적 이진검색트리

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

def optsearchtree (p):
    n = len(p) - 1
    A = [[-1] * (n + 1) for _ in range(n + 2)] # 최소비용
    R = [[-1] * (n + 1) for _ in range(n + 2)] # 루트노드
    for i in range(1, n + 1):
        A[i][i - 1] = 0
        A[i][i] = p[i]
        R[i][i - 1] = 0
        R[i][i] = i
    A[n + 1][n] = 0 # 주대각선은 초기화
    R[n + 1][n] = 0 
    for diagonal in range(1, n): # 대각선을 거치며 최소값 구하기
        for i in range(1, n - diagonal + 1):
            j = i + diagonal 
            # j값은 주 대각선 값(diagonal)만큼 우측에 있어야 하므로 더해준다
            A[i][j], R[i][j] = minimum(A, p, i, j)
    return A, R

# minimum 함수는 연쇄 행렬 곱셈에서 썼던것과 거의 동일
def minimum (A, p, i, j):
    minVal = INF
    minK = 0
    for k in range(i, j + 1):
        value = A[i][k - 1] + A[k + 1][j]
        for m in range(i, j + 1):
            value += p[m]
        if (minVal > value):
            minVal = value
            minK = k
    return minVal, minK

참고: 연쇄 행렬 곱셈 알고리즘

최적 이진검색트리의 노드 순서 구하기

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

def tree (R, i, j):
    k = R[i][j]
    if (k == 0):
        return None
    else:
        node = BSTNode(keys[k])
        node.left = tree(R, i, k - 1)
        node.right = tree(R, k + 1, j)
        return node

class BSTNode:
    def __init__ (self, key):
        self.key = key
        self.left = None
        self.right = None

def preorder (node):
    if (node is None): return
    else: 
        print(node.key, end = ' ')
        preorder(node.left)
        preorder(node.right)

def inorder (node) :
    if (node is None): return
    else:
        inorder(node.left)
        print(node.key, end = ' ')
        inorder(node.right)

자바스크립트로 최적 이진검색트리의 노드 순서 구하기(수정 중)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

const optsearchtree = p => {
    let n = p.length - 1;
    let arr = Array.from(Array(n+2), () => Array(n+1).fill(-1))
    let arr2 = [...arr]
    for (let i = 1; i < n+1; i++){
        arr[i][i-1] = 0
        arr[i][i] = p[i]
        arr2[i][i-1] = 0
        arr2[i][i] = i
    }
    arr[n+1][n] = 0
    arr2[n+1][n] = 0
    for(let diagonal = 1; diagonal < n; diagonal++) {
        for (let i = 1; i < n - diagonal + 1; i++){
            let j = i + diagonal;
            arr[i][j] = minimum(arr, p, i, j).minVal;
            arr2[i][j] = minimum(arr2, p, i, j).minK;
        }
        console.log(arr)
    }
    return { arr: arr, arr2: arr2 }
}

const minimum = (arr, p, i, j) => {
    let minVal = Infinity;
    let minK = 0
    for (let k = i; k < j+1; k++){
        let value = arr[i][k-1] + arr[k+1][j]
        for (let m = i; m < j+1; m++){
            value += p[m]
        }

        if (minVal > value) {
            minVal = value
            minK = k
        }        
    }
    return { minVal: minVal, minK: minK }
}

Comment and share

연쇄 행렬 곱셈

연쇄 행렬 곱셈은 주어진 n개의 연쇄 행렬을 곱하는 최적의 순서를 구하는 문제

• 행렬 곱셈은 결합 법칙이 성립하지만 곱셈 순서에 따라 각 원소의 곱셈 횟수가 달라짐 → 이 곱셈 횟수가 가장 작아지는 최적의 순서를 구하기
• 2 x 3 행렬과 3 x 4 행렬을 곱하면 2 x 4 행렬이 됨
  → i x k 행렬과 k x j 행렬을 곱하면 i x j 행렬이 되며
  → 원소 곱셈의 횟수는 i * k * j가 된다

• Brute-force 방식으로 접근하기
  • 모든 경우의 수(카탈랑 수)를 계산하여 최적의 순서를 선택
  • 카탈랑 수는 결국 지수함수이므로 너무 오래걸림
• Dynamic Programming 방식으로 접근하기
  1. 재귀 관계식을 찾는다
  • M: 연쇄 행렬을 곱하는데 필요한 최소 횟수 행렬
  • M[i][j]: Ai에서 Aj까지 행렬을 곱하는데 필요한 최소 횟수
  • Ai … Aj 행렬을 (Ai … Ak)(Ak+1 … Aj)로 분할하는 재귀 관계식 찾기
  2. 상향식 방법으로 해답을 구하기
  • M[i][i] = 0 (대각선에 위치하는 원소를 0으로 초기화)
  • M[1][n]을 상향식으로 계산 (대각선 1번, 대각선 2번 … 대각선 n-1번)
  • n개의 행렬을 두 개의 최적 부분행렬의 곱으로 분할
  • M[i][j] = minimum(M[i][k] + M[k+1][j] + di-1dkdj) // 단, i ≤ k ≤ j-1

파이썬으로 연쇄 행렬 곱셈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

def minmult (d):
    n = len(d) - 1
    M = [[-1] * (n + 1) for _ in range(n+1)]
    P = [[-1] * (n + 1) for _ in range(n+1)]
    for i in range(1, n + 1):
        M[i][i] = 0
    for diagonal in range(1, n):
        for i in range(1, n - diagonal + 1):
            j = i + diagonal
            M[i][j], P[i][j] = minimum(M, d, i, j)
    return M, P 

def minimum (M, d, i, j):
    minVal = INF
    minK = 0
    for k in range(i, j):
        value = M[i][k] + M[k + 1][j]
        value += d[i -1] * d[k] * d[j]
        if (minVal > value):
            minVal = value
            minK = k
    return minVal, minK

def order(P, i, j):
    if (i == j):
        print('A%d'%(i), end = '')
    else:
        k = P[i][j]
        print('(', end = '')
        order(P, j, k)
        order(P, k + 1, j)
        print(')', end = '')

자바스크립트로 연쇄 행렬 곱셈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

const minmult = d => {
    let n = d.length -1
    let arr = Array.from(Array(n+1), () => Array(n+1).fill(-1))
    let arr2 = [...arr];
    for (let i = 1; i < n+1; i++){
        arr[i][i] = 0;
    }

    for (let diagonal = 1; diagonal < n; diagonal++){
        for (let i = 1; i < n - diagonal + 1; i++){
            j = i + diagonal;
            arr[i][j] = minimum(arr, d, i, j).minVal; 
            arr2[i][j] = minimum(arr, d, i, j).minK; 
        }
    }
    return { result : arr, optimal: arr2 };
}

const minimum = (arr, d, i, j) => {
    let minVal = Infinity;
    for (let k = i; k < j; k++) {
        let value = arr[i][k] + arr[k+1][j] + d[i - 1] * d[k] * d[j]
        if (minVal > value){
            minVal = value;
            minK = k
        }
    }
    return {minVal : minVal, minK : minK}
}

const order = (arr2, i, j) => {
    if (i === j) str += `A${i}`
    else {
        let k = arr2[i][j]
        str += '('
        order(arr2, i, k)
        order(arr2, k+1, j)
        str += ')'
    }
}
/*
예시) 
let d = [5, 2, 3, 4, 6, 7, 8];
let { result, optimal } = minmult(d)
order(optimal, 1, d.length - 1)
console.log(result)
console.log(str) -> `(A1(A2(A3(A4(A5A6)))))`
*/

Comment and share

최단경로와 플로이드 알고리즘

• 최단 경로 문제

  • 주어진 그래프에서 모든 정점의 쌍에 대한 최단 경로를 구하기

  • G = (V, E)일 때, G는 Graph, V는 Vertex set, E는 Edge set

  • G는 방향성, 가중치 그래프로, V1 -6→ V3 와 같은 것을 표로 표현

  • 최단 경로는 단순 경로: 같은 정점을 두 번 거치지 않음

    
    figure 01) 그래프로 표현되는 경우

• 최단 경로 문제의 이해

  • Brute-force로 해결하기
    • 각 정점들에서 다른 정점으로 가는 모든 경로를 구하고
    • 그 경로들 중에서 가장 짧은 경로를 찾는 방법
    • 효율성 분석: 모든 정점간 간선이 존재하면 O(n!)만큼 복잡해진다
  • 최단 경로 문제는 최적화 문제(optimization problem)
    • 최적화 문제는 하나 이상의 해답 후보가 있을 수 있음
    • 그 중에 가장 최적의 값을 가진 해답을 찾는 문제
  • Dynamic programming으로 해결하기
    1. 재귀 관계식을 찾는다
    • D: 각 정점의 쌍이 가지는 최단 경로의 길이를 나타내는 행렬
    • D[i][j]: Vi에서 Vj로 가는 최단 경로의 길이
    • 인접 행렬 W에서 최단 경로의 행렬 D와의 재귀 관계식을 구해야 함
    2. 상향식 방법으로 해답을 구한다
    • D^0^ = W로 초기화, 최종 목표는 D^n^ = D (D^0^, D^1^,…, D^n^)
    3. 행렬의 이해
    • D^k^ : k개의 중간 정점을 지나는 최단 경로 길이의 행렬
    • D^k^[i][j] : vi에서 vj로 k개의 중간 정점을 지나는 최단 경로 길이
    • D^0^ : 다른 어떤 정점도 지나지 않는 최단 경로의 길이 (=W)
    • D^n^ : 다른 모든 정점을 지날 수 있는 최단 경로의 길이 (=D)
    4. 재귀 관계식 구하기
    • D^0^ = W, D^k^는 D^k-1^로부터 구함 (1 ≤ k ≤ n)
    • D^k-1^[i][j]: vi에서 vj로 k-1개의 중간 정점을 지남
    • D^k^[i][j]의 경우
      → 하나의 정점을 더 지나도 최단경로가 없는 경우
      D^k^[i][j] = D^k-1^[i][j]
      → 하나의 정점을 더 지나면 최단경로가 되는 경우
      D^k^[i][j] = D^k-1^[i][k] + D^k-1^[k][j]
      (임의의 경로 = v가 갖는 열 내 k 번째 가중치 + 해당 k번째 v가 갖는 가중치)
    5. 최단 경로의 재귀 관계식
       D^k^[i][j] = min(D^k-1^[i][j], D^k-1^[i][k] + D^k-1^[k][j])

파이썬으로 플로이드 알고리즘

1
2
3
4
5
6
7
8

def floyd (W):
    D = W
    n = len(W)
    for k in range(n):
        for i in range(n):
            for j in range(n):
                D[i][j] = min(D[i][j], D[i][k] + D[k][j])
    return D

자바스크립트로 플로이드 알고리즘

1
2
3
4
5
6
7
8
9

const floyd = W => {
    let arr = [...W];
    let n = W.length;
    for (let k = 0; k < n; k++) 
        for (let i = 0; i < n; i++)  
            for (let j = 0; j < n; j++) 
                arr[i][j] = Math.min(arr[i][j], arr[i][k] + arr[k][j])
    return arr
}

• 최단 길이는 구했으나, 최단 경로는?
  • 최단 경로를 구하기 위해서는 과정을 기록해야 함
  • P[i][j]: vi에서 vj로 가는 최단 경로가 거쳐야 하는 새로운 정점
    • vi에서 vj로 가는 최단 경로 중간에 놓여있는 정점이 최소한 하나 있다면 그 놓여있는 정점 중에서 가장 큰 인덱스
    • 최단 경로의 중간에 놓여있는 정점이 없는 경우에는 -1
  • P[i][j] 값이 -1이라면 간선이 최단경로
  • P[i][j] = k 라면 탐색해서 가장 길이가 짧은 값의 index를 탐색해야 함

파이썬으로 최단 경로 구하기

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

def floyd (W):
    n = len(W)
    D = W
    P = [[-1] * n for _ in range(n)]
    for k in range(n):
        for i in range(n):
            for j in range(n):
                if (D[i][j] > D[i][k] + D[k][j]):
                    D[i][j] = D[i][k] + D[k][j]
                    P[i][j] = k
    return D, P

def path (P, u, v):
    if(P[u][v] != -1):
        path(P, u, P[u][v])
        print('v%d' %(P[u][v]), end = '-> ')
        path(P, P[u][v], v)

D, P = floyd2(W)
for i in range(len(D)):
    print(D[i])
for i in range(len(P)):
    print(P[i])

자바스크립트로 최단 경로 구하기

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

const floydWarshall2 = nodes => {
    let n = nodes.length;
    let arr = [...nodes];
    let route = Array.from(Array(n), () => Array(n).fill(-1));
    for (let k = 0; k < n; k++) 
        for (let i = 0; i < n; i++)  
            for (let j = 0; j < n; j++) {
                if (arr[i][j] > arr[i][k] + arr[k][j]) {
                 arr[i][j] = arr[i][k] + arr[k][j];
                 route[i][j] = k;
                } 
            }
    return { arr: arr, route: route };
}


let { arr, route } = floydWarshall2(nodes)

let str = `v${u}` // u값을 미리 정의한다면 이렇게 사용할 수 있다
const path = (route, u, v) => {
    if (route[u][v] !== -1) {
        path(route, u, route[u][v])
        str += ` → v${route[u][v]}`
        path(route, route[u][v], v);        
    } 
    return str + ` → v${v}`
}

from(itarable obj, map function) 함수를 사용해야 함 fill 함수를 사용하게 될 경우 배열 내 채워지는 모든 배열들의 주소값이 동일한 주소로 입력되기 때문

Comment and share

동적 계획과 이항 계수

수식 깨진 것들은 자체 검색으로 보완할 것

• 동적계획법(Dynamic Programming): 문제를 더 작은 문제로 분할하되 상향식으로 문제를 해결

• 메모이제이션(Memoization): 가장 작은 입력 사례의 해답을 테이블에 저장하고 필요할 때 꺼내 쓴다

• 동적계획법으로 문제 풀기

  1. 문제를 해결할 수 있는 재귀 관계식(점화식)을 구한다
  2. 가장 작은 입력사례로부터 상향식 방법으로 문제를 해결한다

• 분할 정복법 vs 동적 계획법

  • 문제를 작은 사례로 분할하여 해결한다는 점에서 동일
  • Top-Down vs Bottom-Up

• 이항 계수

  • $\binom{n}{k} = \frac{n!}{k!(n-k)!}$, for $0 \le k \le n$
  • $\ n!, k!$의 값은 매우 커서 계산이 어렵다
  • 이항 계수의 재귀적 정의: 분할 정복
  • $\binom{n}{k} = \begin{cases}\binom{n-1}{k-1} + \binom{n-1}{k-1}&0<k<n\{1}&k=0||k=n\end{cases}$

파이썬으로 이항 계수의 재귀적 정의

1
2
3
4
5
6
7
8
9
10

def bin (n, k):
    if (k == 0 or n == k):
        return 1
    else:
        return bin(n - 1, k - 1) + bin(n -1, k)
# 함수 결과를 n = 10까지 출력
for n in range(10):
    for k in range(n + 1):
        print(bin(n, k), end = " ")
    print()

자바스크립트

1
2
3

function bin(n, k) {
    return (k == 0 || k == n) ? 1 : bin(n - 1, k - 1) + bin(n - 1, k);
}

$0 \le k \le n$에 의해 $k$는 $n$보다 큰 값일 수 없다

• 이 방식은 중복 호출이 생김 → 반복적 방법이 요구됨
• 이항 계수의 성질: 파스칼의 삼각형
• 이항 계수 구하기
  1. 재귀 관계식을 찾는다
     $$B[i][j] = \begin{cases}B[i-1][j-1]+B[i-1][j]&0<j<i\1&j=0orj=i\end{cases}$$
  2. 상향식 방법으로 해답을 구한다
     • 파스칼의 삼각형이 가진 특성을 이용한다

파이썬으로 파스칼의 삼각형 구하기

1
2
3
4
5
6
7
8
9
10

def bin2 (n,k):
    B = [[0] * (k + 1) for _ in range(n + 1)]
    for i in range(n + 1):
        for j in range(min(i, k) + 1):
            if (j == 0 or j == i):
                B[i][j] = 1
            else:
                B[i][j] = B[i - 1][j - 1] + B[i - 1][j]
    return B[n][k]
# 출력은 bin(n,k)와 동일

자바스크립트로 파스칼의 삼각형 구하기

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

function bin2(n) {
    let result = []; // 빈 배열을 선언
    for (let row = 1; row <= n; row++) {
        // 행 수 만큼 for 루프
        let arr = [];
        // 추가할 새 배열을 선언 (루프 돌면서 초기화됨)
        for (let col = 0; col < row; col++) {
            if (col === 0 || col === row - 1) 
                // 파스칼의 삼각형에서 처음과 맨 마지막 숫자는 1로 채운다
                arr.push(1);
             else 
                // 안쪽 숫자는 이미 result 배열에 추가된 이전 열의 연속된 숫자를 더함
                arr.push((result[row-2][col-1] + result[row-2][col]));
        }
        result.push(arr);
    }
    return result
}

• 이항 계수의 시간 복잡도와 성능 개선
  • $k$가 $n/2$보다 클 경우, 나머지 절반 삼각형은 중복값
  • 1차원 배열만으로도 구현이 가능

파이썬으로 파스칼의 삼각형 성능개선

1
2
3
4
5
6
7
8
9
10
11
12

def bin3 (n,k):
    if (k > n // 2):
        k = n - k
    B = [0] * (k + 1)
    B[0] = 1
    for i in range(1, n + 1):
        j = min(i, k)
        while (j > 0):
            B[j] = B[j] + B[j - 1]
            j -= 1
    return B[k]
# 출력은 bin(n,k)와 동일

자바스크립트로 파스칼의 삼각형 성능개선

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

function bin3(n,k) {
    if(n === 1) return [1] // n이 1일때엔 [1]을 리턴하도록 함
    // 파스칼의 삼각형은 절반 이후로는 전반 절반과 같은 값이다
    if(k > Math.floor(n/2)) k = n - k
    // 배열을 k+1 길이만큼 생성하고 0으로 채운다
    let arr = Array(k+1).fill(0)
    // 첫번째 값을 1로 설정한다
    arr[0] = 1;
    for (let i = 1; i < n + 1; i++){
        let j = Math.min(i, k)
        while (j > 0) {
            arr[j] = arr[j] + arr[j-1] // 이전값과 더한 값
            j -= 1 // j를 줄여나간다
        }
    }
    // 파스칼 삼각형 열이 홀수라면 중간 숫자는 중복되는 숫자이므로 slice함
    return n % 2 !== 0 
        ? [...arr, ...arr.slice(0,-1).reverse()] 
        : [...arr, ...arr.reverse()]
}

Comment and share

큰 정수의 계산

• 특정 컴퓨터/언어가 표현할 수 없는 큰 정수의 산술 연산은 어떻게 할까?
• int값은 대부분 32bit (부호값 1bit + 31bit) 이므로 -2^32^ ~ 2^31^-1까지만 표현 가능
• 가정: 10진수 체계에서의 덧셈과 곱셈
• 10진수를 소프트웨어적으로 표현하는 법 : 리스트를 이용하여 각 자리수를 하나의 원소로 저장 (예: 567,832: S = [2,3,8,7,6,5])
  :point_right: 참고 자바스크립트가 숫자를 다루는 법
  • 자바스크립트에는 number라는 하나의 숫자형만 존재하며 이는 64비트 2진 부동소수점 타입
  • 1개의 부호비트와 11비트의 지수, 53비트의 유효 숫자로 구성됨
  • Number.MAX_SAFE_INTEGER = 9007199254740991
  • 예로 숫자 9000000000000000000 는 ["+", 8650752, 7098594, 31974]로 표현된다

큰 정수의 덧셈

• n개의 자릿수 각각을 더하면서 올림수(carry)를 고려

파이썬으로 정수 더하기

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

def ladd (u, v):
    n = len(u) if (len(u) > len(v)) else len(v) 
    # 파이썬에서 타 언어의 삼항연산자 처럼 쓰는 법
    # (u.length > v.length) ? n = u.length : n = v.length; 같은 것
    result = []
    carry = 0
    for k in range(n):
        i = u[k] if(k < len(u)) else 0
        j = v[k] if(k < len(v)) else 0
        value = i + j + carry
        carry = value // 10
        result.append(value % 10)
    if (carry > 0):
        result.append(carry)
    return result

자바스크립트로 정수 더하기

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

const add = (a, b) => {
    let n = 0;
    (a.length > b.length) ? n = a.length : n = b.length;
    let result = [];
    let carry  = 0;
    for (let k = 0; k < n; k++) {
        let i = 0, j = 0
        
        if (k < a.length) i = a[k]
        else              i = 0;
        if (k < b.length) j = b[k]
        else              j = 0;

        let value = i + j + carry;
        carry = Math.floor(value / 10)
        result.push(value % 10)
    }
    if (carry > 0) result.push(carry);
    return Number(result.reverse().join(''))
}

큰 정수의 곱셈

• Brute-Force 방법 : O(n^2^)
• Divide-and-Conquer
  • u (n자리) = *x * 10^m^* (n/2자리) + y (n/2자리)
  • uv = (x * 10^m^** + y)(**w * 10^m^ + z)
    → uv = xw * 10^2m^ + (xy + yw) * 10^m^ + yz

파이썬으로 정수 곱하기

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

def prod(u, v):
    n = len(u) if (len(u) > len(v)) else len(v) 
    if (len(u) == 0 or len(v) == 0):
        return [0]
    elif (n <= threshold):
        return lmult(u, v)
    else:
        m = n // 2
        # divide
        x = div(u, m); y = rem(u, m)
        w = div(v, m); z = rem(v, m)
        # conquer
        p1 = prod(x, w) # xw
        p2 = ladd(prod(x, z), prod(w, y)) # (xy + yw)
        p3 = prod(y, z) # yz
        return ladd(ladd(exp(p1, 2*m), exp(p2, m)), p3)

def exp(u, m):
    if(u == [0]):
        return [0]
    else:
        return ([0] * m) + u
         # 배열의 합은 두 배열을 단순히 합하는 것
         # ex) [0, 0, 0] + [5, 6, 7] = [0, 0, 0, 5, 6, 7]

def div(u, m):
    if(len(u) < m):
        u.append(0)
    return u[m : len(u)]

def rem(u, m):
    if(len(u) < m):
        u.append(0)
    return u[0 : m]

def lmult (u, v):
    i = u[0] if (0 < len(u)) else 0
    j = v[0] if (0 < len(v)) else 0
    value = i * j
    carry = value // 10
    result = []
    result.append(value % 10)
    if(carry > 0):
        result.append(carry)
    return result

곱셈 개선

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

def prod2(u, v):
    n = len(u) if (len(u) > len(v)) else len(v) 
    if (len(u) == 0 or len(v) == 0):
        return [0]
    elif (n <= threshold):
        return lmult(u, v)
    else:
        m = n // 2
    
        x = div(u, m); y = rem(u, m)
        w = div(v, m); z = rem(v, m)

        # 이 부분이 바뀜
        r = prod2(ladd(x, y), ladd(w, z))
        
        p1 = prod2(x, w) # xw
        p3 = prod2(y, z) # yz

         # 이 부분이 바뀜
        p2 = lsub(r, ladd(p1, p3)) # (xy + yw)
        return ladd(ladd(exp(p1, 2*m), exp(p2, m)), p3)

def lsub (u, v):
    n = len(u) if (len(u) > len(v)) else len(v)
    result = []
    borrow = 0
    for k in range(n):
        i = u[k] if (k < len(u)) else 0
        j = v[k] if (k < len(v)) else 0
        value = i - j + borrow
        if (value < 0):
            value += 10
            borrow = -1
        else:
            borrow = 0
        result.apeend(value % 10)
    if(borrow < 0):
        print("음의 정수는 처리할 수 없음")
    return result

# 나머지 함수는 동일

Comment and share

슈트라센 행렬 곱셈

• 단순 참고용으로만 공부함 (행렬 계산은 어려워…)

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70

  def strassen (A, B): n = len(A) if (n <= threshold): return matrixmult(A,B) A11, A12, A21, A22 = divide(A) B11, B12, B21, B22 = divide(B) M1 = strassen(madd(A11, A22), madd(B11, B22)) M2 = strassen(madd(A21, A22), B11) M3 = strassen(A11, msub(B12, B22)) M4 = strassen(A22, madd(B21, B11)) M5 = strassen(madd(A11, A12), B22) M6 = strassen(madd(A21, A11), madd(B11, B12)) M7 = strassen(madd(A12, A22), madd(B21, B22)) return conquer(M1, M2, M3, M4, M5, M6, M7) def divide (A): n = len(A) m = n // 2 A11 = [[0] * m for _ in range(m)] A12 = [[0] * m for _ in range(m)] A21 = [[0] * m for _ in range(m)] A22 = [[0] * m for _ in range(m)] for i in range(m): for j in range(m): A11[i][j] = A[i][j] A12[i][j] = A[i][j + m] A21[i][j] = A[i + m][j] A22[i][j] = A[i + m][j + m] return A11, A12, A21, A22 def conquer(M1, M2, M3, M4, M5, M6, M7): C11 = madd(msub(madd(M1, M4), M5), M7) C12 = madd(M3, M5) C21 = madd(M2, M4) C22 = madd(msub((madd(M1, M3), M2), M6) m = len(C11) n = 2 * m C = [[0] * n for _ in range(n)] for i in range(m): for j in range(m): C[i][j] = C11[i][j] C[i][j + m] = C12[i][j] C[i + m][j] = C21[i][j] C[i + m][j + m] = C22[i][j] return C def madd(A, B): n = len(A) C = [[0] * n for _ in range(n)] for i in range(n): for j in range(n): C[i][j] = A[i][j] + B[i][j] return C def msub (A, B): n = len(A) C = [[0] * n for _ in range(n)] for i in range(n): for j in range(n): C[i][j] = A[i][j] - B[i][j] return C def matrixmult (A, B): n = len(A) C = [[0] * n for _ in range(n)] for i in range(n): for j in range(n): for k in range(n): C[i][j] += A[i][k] * B[k][j] return C

  자바스크립트에서 행렬계산 (참고용)
• map과 reduce를 사용하여 iterable 객체를 돌며 행렬을 계산
• 단순 덧셈은 하나의 행렬을 돌며 두번째 인수로 인덱스를 받아 double for문 처럼 사용

  1 2 3 4 5 6 7 8 9 10 11 12 13

  function sumMatrix (arr1, arr2) { return arr1.map((arr, i) => arr.map((v, j) => v + arr2[i][j])) } function multiplyMatrix(arr1, arr2) { return arr1.map( row => row.map( // x = arr[0] 값, y = index 값 (_, i) => row.reduce( // reduce는 (acc, cur, index) (sum, cell, j) => sum + cell * arr2[j][i], 0))) }

Comment and share

퀵정렬

• 내부정렬 : 추가적인 리스트를 사용하지 않는 정렬(Quick Sort Algorithm: Hoare, 1962)
• 퀵정렬

  Divide: 기준 원소를 정해서 좌우로 분할
  Conquer: 왼쪽/오른쪽 리스트를 각각 재귀적으로 정렬
  Obtain: 정렬된 리스트를 리턴

파이썬으로 퀵정렬

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

def quicksort(S, low, high):
    if (high > low):
        pivotpoint = partition(S, low, high)
        quicksort(S, low, pivotpoint - 1)
        quicksort(S, pivotpoint + 1 , high)

def partition(S, low, high):
    pivotitem = S[low]
    j = low
    for i in range(low + 1, high + 1):
        if(S[i] < pivotitem):
            j += 1;
            S[i], S[j] = S[j], S[i] # swap 2 items
    pivotpoint = j
    S[low], S[pivotpoint] = S[pivotpoint], S[low] # swap 2 items
    return pivotpoint

• 기준원소(pivotpoint)를 어떻게 정할까? : 편의상 첫 원소를 기준 원소로 정한다
• 두 개의 인덱스(i, j)를 이용해서 비교하고 교환한다

자바스크립트로 퀵정렬 (기준 원소가 배열의 맨마지막 요소일 때)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

function quickSort (arr, start, end) {
    if (start >= end) return;

    let index = partition(arr, start, end);
    quickSort(arr, start, index - 1);
    quickSort(arr, index + 1, end)

}

function partition (arr, start = 0, end = arr.length - 1) {
    let pivotIndex = start;
    let pivotValue = arr[end];
    for(let i = start; i < end; i++){
        if(arr[i] < pivotValue) {
            swap(arr, i, pivotIndex);
            pivotIndex++
        }
    }
    swap(arr, pivotIndex, end);
    return pivotIndex;
}

function swap (arr, a, b) {
    let temp = arr[a];
    arr[a] = arr[b];
    arr[b] = temp;
}

참고영상 : Coding Challenge #143​: Quicksort Visualization

퀵정렬(분할 교환 정렬)

파이썬으로 퀵정렬 할 때 다른 방법으로 파티션 구하기

1
2
3
4
5
6
7
8
9
10
11
12
13
14

def partition2 (S, low, high):
    pivotitem = S[low]
    i = low + 1
    j = high
    while (i <= j):
        while (S[i] < pivotitem):
            i += 1
        while (S[j] > pivotitem):
            j -= 1
        if (i < j):
            S[i], S[j] = S[j], S[i] # swap 2 items
        pivotpoint = j
        S[low], s[pivotpoint] = S[pivotpoint], S[low] # swap 2 items 
        return pivotpoint

자바스크립트로 퀵정렬 할 때 다른 방법으로 파티션 구하기

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

function partition2 (array, start, end) {
    // 맨 마지막이나 맨 처음으로 설정했던 pivot값을 배열의 중간값으로 설정
	const pivotValue = array[ Math.floor((start + end) / 2) ];

    // 양 끝의 인덱스를 하나씩 늘리거나 하나씩 줄이면서
    // 피봇값보다 작은 값인 start와 피봇값보다 큰 값인end값을 구함
	while (start <= end) { 
		while (array[start] < pivotValue) start = start + 1;
		while (array[end] > pivotValue) end = end - 1;
        
        // start값이 end값보다 크단 뜻은 배열을 한번 다 돌았다는 뜻임
		if (start <= end) { 
            // 이 구문을 들어온다는 뜻은 배열을 돌면서 pivotValue보다 
            // 큰 값(array[start]값)과 작은 값(array[end]값)의 두 값을 교체해줌
			swap(array, start, end);
			start = start + 1;
			end = end - 1;
		}
	}
    // 이 과정이 끝나면 pivotValue보다 작은 값은 왼쪽에, 큰 값은 오른쪽으로 정렬되었단 뜻이므로 
    // 해당 인덱스 값을 리턴하여 다시 배열을 둘로 쪼갬
	return start; 
}

Comment and share

이분검색(Binary search)

• 정렬되지 않은 리스트에서 주어진 키가 존재하는가? - 순차 탐색
• 정렬된 리스트에서 주어진 키가 존재하는가? - 이분 검색

• 이분검색의 알고리즘 설계방식: 분할정복(Divide-and-Conquer)

    :point_right: 정렬된 리스트 S에 어떤 키 x가 존재하는가?
    :point_right: 존재하면 S에서 x의 위치, 아니면 -1을 리턴
  

  S의 정가운데 원소와 x를 비교하여 같으면 해당 위치를 리턴 아니라면,
  Divide: 정 가운데 원소를 기준으로 S를 두개의 리스트로 분할
  Conquer: x가 정가운데 원소보다 크면 오른쪽, 작으면 왼쪽을 재귀 호출
  Obtain: 선택한 리스트에서 얻은 답을 리턴

파이썬으로 이분검색

1
2
3
4
5
6
7
8
9
10
11

def location (S, low, high):
    if (low > high):
        return 0
    else:
        mid = (low + high) // 2
        if (x == S[mid]):
            return mid
        elif (x < S[mid]):
            return location(S, low, mid -1)
        else:
            return location(S, mid+1, high)

자바스크립트로 이분검색

1
2
3
4
5
6
7
8
9
10

function location(arr, low = 0, high = arr.length) {     
    if(low > high) 
        return 0
    else {
        let mid = Math.floor((low + high) / 2);
        if(x === arr[mid]) return mid;
        else if (x < arr[mid]) return location(arr, low, mid-1);
        else return location(arr, mid+1, high);
    }
}

강의 내에서 x값은 전역변수를 사용하였음

합병정렬

• 합병정렬의 알고리즘 설계방식: 분할정복(Divide-and-Conquer)

  Divide: 원소가 n개인 S를 n/2개의 원소를 가진 두 개의 리스트로 분할
  Conquer: 왼쪽의 리스트와 오른쪽의 리스트를 각각 재귀적으로 합병정렬
  Obtain: 각각 정렬된 두 개의 리스트를 정렬된 하나의 리스트로 합병하여 리턴

합병정렬 예시

파이썬으로 합병정렬

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

def mergesort (S):
    n = len(S)
    if (n <= 1):
        return S
    else:
        mid = n // 2
        U = mergesort(S[0 : mid])
        V = mergesort(S[mid: n])
        return merge(U, V)

def merge(U, V):
    S = []
    i = j = 0
    while (i < len(U) and j < len(V)):
        if(U[i] < V[j]):
            S.append(U[i])
            i += 1
        else:
            S.append(V[j])
            j += 1
    if (i < len(U)):
        S += U[i : len(U)]
    else:
        S += V[j : len(V)]
    return S

자바스크립트로 합병정렬

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

function mergesort (arr) {
    if(arr.length === 1) return arr;
    
    let mid = Math.floor(arr.length/2);
    let leftSide = arr.slice(0, mid)
    let rightSide = arr.slice(mid)
    
    return merge(mergesort(leftSide), mergesort(rightSide));
    
}

function merge(left, right) {
    let result = [];
    while (left.length !== 0 && right.length !== 0) {
		left[0] <= right[0] 
        ? result.push(left.shift()) 
        : result.push(right.shift());
	}

    return [...result, ...left, ...right];
}

• 합병정렬의 문제점
  • 배열을 추가적으로 사용하게 됨 → 메모리 사용의 비효율성

합병정렬의 효율화

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

def mergesort2 (S, low, high):
    if(low < high):
        mid = (low + high) // 2
        mergesort2(S, low, mid)
        mergesort2(S, mid + 1, high)
        merge2(S, low, mid, high)

def merge2(S, low, mid, high):
    U = []
    i = low
    j = mid +1
    while (i <= mid and j <= high):
        if (S[i] < S[j]):
            U.append(S[i])
            i += 1
        else:
            U.append(S[j])
            j += 1
    if (i <= mid):
        U += S[i : mid + 1]
    else:
        U += S[j : high + 1]
    for k in range(low, high +1):
        S[k] = U[k -low]

자바스크립트로 합병정렬 조금 더 생각해보기

1
2
3
4
5
6
7
8
9
10
11
12

// 파이썬처럼 배열을 덜 정의하면서 효율적으로 구현하는 법은 더 검색해볼 것
function mergesort (arr) {
    if(arr.length === 1) return arr;
    
    let mid = Math.floor(arr.length/2);
    let leftSide = arr.splice(0, mid)
    // splice함수를 사용하면 arr를 조작하므로 
    // arr에는 자동적으로 rightSide만 남게 됨

    return merge(mergesort(leftSide), mergesort(arr));    
}
// merge 함수는 상동하므로 생략

Comment and share

문제

실패율은 다음과 같이 정의한다.
스테이지에 도달했으나 아직 클리어하지 못한 플레이어의 수 / 스테이지에 도달한 플레이어 수

전체 스테이지의 개수 N, 게임을 이용하는 사용자가 현재 멈춰있는 스테이지의 번호가 담긴 배열 stages가 매개변수로 주어질 때, 실패율이 높은 스테이지부터 내림차순으로 스테이지의 번호가 담겨있는 배열을 return 하도록 solution 함수를 완성하라.

통과한 코드 예시

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

function solution(N, stages) {
    let answer = [];
    for(let i = 1; i <= N; i++) {
      let thisStageFailRate = stages.filter(s => s === i).length
      let otherUserFailRate = stages.filter(s => s >= i).length
      if (thisStageFailRate === 0) {
        answer.push({stage: i, failRate: 0});
      } else {
        answer.push({stage: i, failRate: thisStageFailRate/otherUserFailRate});
      }
    }

    return answer.sort((a,b) => (b.failRate === a.failRate) 
                       ? a.stage - b.stage : b.failRate - a.failRate)
                 .map(each => each.stage);
}

처음에 잘못 생각했던 것

1. 실패율을 계산할 때 해당 스테이지를 클리어하지 못한 사용자 / 전체 사용자로 계산했던 것
   => 현재 스테이지를 클리어하지 못한 사용자 / 현 스테이지보다 높은 스테이지로 넘어간 사용자 수 로 계산해야 했음
2. 실패율만 배열에 push 했던 것
   => 배열에 스테이지값과 실패율을 각각 갖는 객체를 push하여 객체 내 실패율로 sort한 후에 스테이지 값을 return할 수 있도록 map 함수를 사용해야 했음

Comment and share